
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<![]() )的图象与x轴的交点中,相邻两条对称轴之间的距离为
)的图象与x轴的交点中,相邻两条对称轴之间的距离为![]() ,且图象上一个最低点为M
,且图象上一个最低点为M![]() .
.
(1)求ω,φ的值;
(2)求f(x)的图像的对称中心;
(3)当x∈![]() 时,求f(x)的值域.
时,求f(x)的值域.
【答案】(1)ω=2, φ=![]() (2)见解析(3)[-1,2]
(2)见解析(3)[-1,2]
【解析】
(1) 由最低点为M![]() 得A=2. 由相邻的两条对称轴之间的距离为
得A=2. 由相邻的两条对称轴之间的距离为![]() 求出ω的值,再根据最小值点求出φ=
求出ω的值,再根据最小值点求出φ=![]() .(2)令
.(2)令![]() 求出函数的对称中心.(3)先求出 2x+
求出函数的对称中心.(3)先求出 2x+![]() ∈
∈![]() ,再利用三角函数的图像和性质求出函数的最大值和最小值,即得函数的值域.
,再利用三角函数的图像和性质求出函数的最大值和最小值,即得函数的值域.
(1)由最低点为M![]() 得A=2.
得A=2.
由相邻的两条对称轴之间的距离为![]() 得
得![]() =
=![]() ,即T=π,ω=
,即T=π,ω=![]() =
=![]() =2,
=2,
由点M![]() 在图象上得
在图象上得![]() ,
,
即![]() ,故
,故![]() +φ=2kπ-
+φ=2kπ-![]() ,k∈Z,所以φ=2kπ-
,k∈Z,所以φ=2kπ-![]() ,k∈Z,
,k∈Z,
因为0<φ<![]() ,所以φ=
,所以φ=![]() .
.
(2)令![]() ,
,
所以f(x)的图像的对称中心为![]() .
.
(3)因为x∈![]() ,所以2x+
,所以2x+![]() ∈
∈![]() .
.
当2x+![]() =
=![]() ,即x=
,即x=![]() 时,f(x)取得最大值2;
时,f(x)取得最大值2;
当2x+![]() =
=![]() ,即x=
,即x=![]() 时,f(x)取得最小值-1,
时,f(x)取得最小值-1,
故f(x)的值域为[-1,2].


科目:高中数学 来源: 题型:
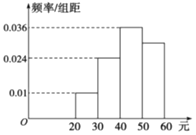
【题目】某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在![]() 元的学生有60人,则下列说法正确的是______.
元的学生有60人,则下列说法正确的是______.
A.样本中支出在![]() 元的频率为
元的频率为![]()
B.样本中支出不少于40元的人数有132
C.n的值为200
D.若该校有2000名学生,则定有600人支出在![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将现有![]() 名男生和
名男生和![]() 名女生站成一排照相.(用数字作答)
名女生站成一排照相.(用数字作答)
(1)两女生相邻,有多少种不同的站法?
(2)两名女生不相邻,有多少种不同的站法?
(3)女生甲不在左端,女生乙不在右端,有多少种不同的站法?
(4)女生甲要在女生乙的右方(可以不相邻)有多少种不同的站法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(n)=1+ ![]() +
+ ![]() +…+
+…+ ![]() (n∈N*),计算可得f(2)=
(n∈N*),计算可得f(2)= ![]() ,f(4)>2,f(8)>
,f(4)>2,f(8)> ![]() ,f(16)>3,f(32)>
,f(16)>3,f(32)> ![]() ,推测当n≥2时,有 .
,推测当n≥2时,有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga( ![]() ﹣mx)在R上为奇函数,a>1,m>0. (Ⅰ)求实数m的值;
﹣mx)在R上为奇函数,a>1,m>0. (Ⅰ)求实数m的值;
(Ⅱ)指出函数f(x)的单调性.(不需要证明)
(Ⅲ)设对任意x∈R,都有f( ![]() cosx+2t+5)+f(
cosx+2t+5)+f( ![]() sinx﹣t2)≤0;是否存在a的值,使g(t)=a
sinx﹣t2)≤0;是否存在a的值,使g(t)=a ![]() ﹣2t+1最小值为﹣
﹣2t+1最小值为﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数y=Asin(ωx+φ)(A<0,ω>0,|φ|≤ ![]() )图象的一部分.为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( )
)图象的一部分.为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( ) 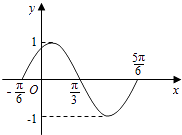
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
B.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
D.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2asinωxcosωx+2 ![]() cos2ωx﹣
cos2ωx﹣ ![]() (a>0,ω>0)的最大值为2,且最小正周期为π. (I)求函数f(x)的解析式及其对称轴方程;
(a>0,ω>0)的最大值为2,且最小正周期为π. (I)求函数f(x)的解析式及其对称轴方程;
(II)若f(α)= ![]() ,求sin(4α+
,求sin(4α+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 是直线
是直线![]() 上的动点,定点
上的动点,定点![]() 点
点![]() 为
为![]() 的中点,动点
的中点,动点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程
的方程
(2)过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() 两点,
两点,![]() 为
为![]() 上任意一点,直线
上任意一点,直线![]() 交
交![]() 于
于![]() 两点,以
两点,以![]() 为直径的圆是否过
为直径的圆是否过![]() 轴上的定点? 若过定点,求出定点的坐标;若不过定点,说明理由。
轴上的定点? 若过定点,求出定点的坐标;若不过定点,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com