
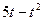 (百万元)。
(百万元)。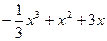 (百万元),请设计资金分配方案,使该公司由
(百万元),请设计资金分配方案,使该公司由 此获得的收益最大。(注:收益=销售额—投入)
此获得的收益最大。(注:收益=销售额—投入) 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源:不详 题型:单选题
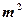 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度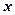 不得
不得 超过
超过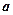 米,房屋正面的造价为400元
米,房屋正面的造价为400元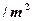 ,房屋侧面的造价为150元
,房屋侧面的造价为150元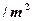 ,屋顶和底面的造价费用合计为5800元,如果墙高为3米.且不计房屋背面的费用.
,屋顶和底面的造价费用合计为5800元,如果墙高为3米.且不计房屋背面的费用. 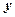 表示成
表示成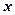 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
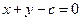 与曲线
与曲线 有2个交点,则实数
有2个交点,则实数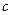 的最小值是 ( )
的最小值是 ( )| A.2 | B.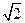 | C.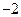  | D.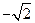 82615980 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
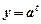 (t≥0,a>0且a≠1).有以下叙述 ①第4个月时,剩留量就会低于
(t≥0,a>0且a≠1).有以下叙述 ①第4个月时,剩留量就会低于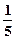 ;②每月减少的有害物质量都相等;③若剩留量为
;②每月减少的有害物质量都相等;③若剩留量为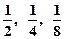 所经过的时间分别是
所经过的时间分别是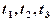 ,则
,则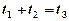 . 其中所有正确的叙述是
. 其中所有正确的叙述是| A.①②③ | B.①② | C.①③ | D.②③ |
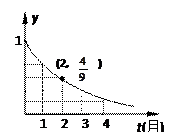
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com