
【题目】已知椭圆C:![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线![]() 上任意一点,过F作TF的垂线交椭圆C于点P,Q.
上任意一点,过F作TF的垂线交椭圆C于点P,Q.
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当![]() 最小时,求点T的坐标.
最小时,求点T的坐标.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求曲线C的极坐标方程和直线l的直角坐标方程;
(2)若射线![]() 与曲线C交于点A(不同于极点O),与直线l交于点B,求
与曲线C交于点A(不同于极点O),与直线l交于点B,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三台机器是否需要照顾相互之间没有影响.已知在某1 h内,甲、乙都需要照顾的概率为0.05,甲、丙都需要照顾的概率为0.1,乙、丙都需要照顾的概率为0.125.
(1)求甲、乙、丙每台机器在这1 h内需要照顾的概率分别是多少?
(2)计算这1 h内至少有一台机器需要照顾的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是一个首项为2,公比为q(q![]() 1)的等比数列,且3a1,2a2,a3成等差数列.
1)的等比数列,且3a1,2a2,a3成等差数列.
(1)求{an}的通项公式;
(2)已知数列{bn}的前n项和为Sn,b1=1,且![]() 1(n≥2),求数列{an
1(n≥2),求数列{an![]() bn}的前n项和Tn.
bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的周期为
)的周期为![]() ,图像的一个对称中心为
,图像的一个对称中心为![]() ,将函数
,将函数![]() 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移
图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像.
的图像.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)是否存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定![]() 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
(3)求实数a与正整数n,使得![]() 在
在![]() 内恰有2013个零点.
内恰有2013个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四位同学参加三项不同的竞赛.
(1)每位同学必须参加一项,有几种不同结果?
(2)每项竞赛只有且必须有一位同学参加,有几种不同结果?
(3)每位同学最多参加一项,且每项竞赛只许有一位同学参加,有几种不同结果?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2. 若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 .
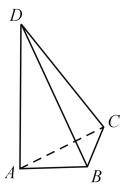
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行了全体学生的一分钟跳绳比赛,为了了解学生的体质,随机抽取了100名学生,其跳绳个数的频数分布表如下:
一分钟跳绳个数 |
|
|
|
|
|
|
|
频数 | 6 | 12 | 18 | 30 | 16 | 10 | 8 |
(1)若将抽取的100名学生一分钟跳绳个数作为一个样本,请将这100名学生一分钟跳绳个数的频率分布直方图补充完整(只画图,不需要写出计算过程);
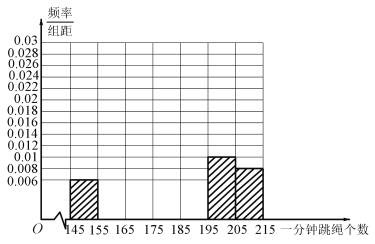
(2)若该校共有3000名学生,所有学生的一分钟跳绳个数X近似服从正态分布![]() ,其中
,其中![]() 为样本平均数的估计值(同一组中的数据用该组区间的中点值为代表).利用所得正态分布模型,解决以下问题:
为样本平均数的估计值(同一组中的数据用该组区间的中点值为代表).利用所得正态分布模型,解决以下问题:
①估计该校一分钟跳绳个数超过165个的人数(结果四舍五入到整数);
②若在该校所有学生中任意抽取4人,设一分钟跳绳个数超过180个的人数为![]() ,求随机变量
,求随机变量![]() 的分布列、期望与方差./span>
的分布列、期望与方差./span>
附:若随机变量Z服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com