
如图,在正三棱柱![]() 中,D是BC的中点,
中,D是BC的中点,![]() 。
。
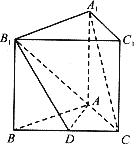
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求点C到平面![]() 的距离。
的距离。
解:(1)连接![]() ,设
,设![]() ,连接DE,如图所示。
,连接DE,如图所示。
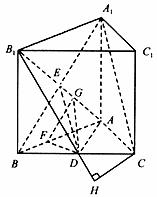
∵![]() 是正三棱柱, 且
是正三棱柱, 且![]()
∴四边形![]() 是正方形,
是正方形,
∴E是![]() 的中点,又D是BC的中点,
的中点,又D是BC的中点,
∴ ![]() ∥
∥![]() 。
。
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() 。
。
(2)在平面ABC内作DF⊥AB于点F,在平面![]() 内作FG ⊥
内作FG ⊥![]() 于点G,连接DG。
于点G,连接DG。
∵平面![]() ⊥平面ABC,
⊥平面ABC,
∴DF⊥平面![]() ,
,
∴FG是DG在平面![]() 上的射影,
上的射影,
∵FG⊥![]() ,∴ DG⊥
,∴ DG⊥![]() 。
。
∴∠FGD是二面角![]() 的平面角。
的平面角。
设![]() ,
,
在正![]() 中,
中,![]()
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
所以,二面角![]() 的大小为
的大小为![]() 。
。
(3)∵平面![]() ⊥平面ABC,且AD⊥BC,
⊥平面ABC,且AD⊥BC,
∴AD⊥平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() ⊥平面
⊥平面![]() 。
。
在平面![]() 内作CH⊥
内作CH⊥![]() 交
交![]() 的延长线于点H。
的延长线于点H。
则CH的长度就是点C到平面![]() 的距离。
的距离。
由![]() ∽
∽![]() ,得
,得![]() 。
。
即点C到平面![]() 的距离是
的距离是![]() 。
。


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
 如图,在正三棱柱中,AB=2,AA1=2由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线与棱AA1的交点记为M,求:
如图,在正三棱柱中,AB=2,AA1=2由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线与棱AA1的交点记为M,求:| A1M | AM |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟冲刺理科数学试卷(二)(解析版) 题型:解答题
如图,在正三棱柱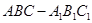 中,
中, ,
, 是
是 的中点,
的中点, 是线段
是线段 上的动点(与端点不重合),且
上的动点(与端点不重合),且 .
.

(1)若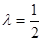 ,求证:
,求证: ;
;
(2)若直线 与平面
与平面 所成角的大小为
所成角的大小为 ,求
,求 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com