
分析 (1)若f(x)=log2(ax2+ax+1)的定义域为R,则ax2+ax+1>0恒成立,故a=0,或$\left\{\begin{array}{l}a>0\\△={a}^{2}-4a<0\end{array}\right.$,解得实数a的取值范围;
(2)若函数f(x)=log2(ax2+2ax+3)的值域为(-∞,0],则t=ax2+2ax+3有最小值1,故$\left\{\begin{array}{l}a>0\\ \frac{12a-4{a}^{2}}{4a}=1\end{array}\right.$,解得a值;
(3)若函数f(x)=log2(x2+2ax+a+1)在区间(0,1]上递增,则t=x2+2ax+a+1在区间(0,1]上递增,且t=x2+2ax+a+1>0在区间(0,1]上恒成立,故$\left\{\begin{array}{l}-a≤0\\ a+1≥0\end{array}\right.$,解得实数a的取值范围.
解答 解:(1)若f(x)=log2(ax2+ax+1)的定义域为R,
则ax2+ax+1>0恒成立,
故a=0,或$\left\{\begin{array}{l}a>0\\△={a}^{2}-4a<0\end{array}\right.$,
解得:a∈[0,4);
(2)若函数f(x)=log2(ax2+2ax+3)的值域为(-∞,0],
则t=ax2+2ax+3有最小值1,故$\left\{\begin{array}{l}a>0\\ \frac{12a-4{a}^{2}}{4a}=1\end{array}\right.$,解得:a=2,
(3)若函数f(x)=log2(x2+2ax+a+1)在区间(0,1]上递增,
则t=x2+2ax+a+1在区间(0,1]上递增,且t=x2+2ax+a+1>0在区间(0,1]上恒成立,
故$\left\{\begin{array}{l}-a≤0\\ a+1≥0\end{array}\right.$,解得:a≥0
点评 本题考查的知识点是函数恒成立问题,对数函数的图象和性质,转化思想,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>b,则a2>b2”的否命题是“若a<b,则a2<b2” | |
| B. | 命题“若a>b,则a2>b2”的逆命题是“若a≤b,则a2≤b2” | |
| C. | 命题“?x∈R,cosx<1”的否定命题是“?x0∈R,cosx0≥1” | |
| D. | 命题“?x∈R,cosx<1”的否定命题是“?x0∈R,cosx0>1” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{PC}$和$\overrightarrow{BD}$ | B. | $\overrightarrow{DA}$和$\overrightarrow{PB}$ | C. | $\overrightarrow{PD}$与$\overrightarrow{AB}$ | D. | $\overrightarrow{PC}$与$\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
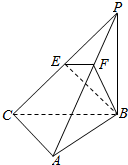 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | 20 | 40 | 70 | 50 | 20 | 200 |
| 女生 | 男生 | 总计 | |
| 及格人数 | 60 | ||
| 不及格人数 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
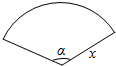 如图,用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地,设扇形的半径为xm,面积为Scm2.
如图,用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地,设扇形的半径为xm,面积为Scm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com