
【题目】如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
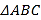
(1)设AD=x(x≥1),ED=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为 ![]() ,赔钱的概率是
,赔钱的概率是 ![]() ;乙股票赚钱的概率为
;乙股票赚钱的概率为 ![]() ,赔钱的概率为
,赔钱的概率为 ![]() .对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元.
.对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元.
(Ⅰ)求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
(Ⅱ)试求袁先生2016年上半年同事投资甲、乙两只股票的总收益的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知3acosA=ccosB+bcosC.
(1)求cosA,sinA的值;
(2)若cosB+cosC= ![]() ,求cosC+
,求cosC+ ![]() sinC的值.
sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=AD=a,E为CD上任意一点.
(I)求证:B1E⊥AD1;
(Ⅱ)若CD= ![]() a,是否存在这样的E点,使得AD1与平面B1AE成45°的角?说明理由.
a,是否存在这样的E点,使得AD1与平面B1AE成45°的角?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 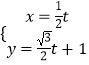 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 ![]() (θ为参数)
(θ为参数)
(1)以原点O为极点,以x轴正半轴为极轴(与直角坐标系xOy取相同的长度单位)建立极坐标系,若点P的极坐标为(4, ![]() ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,利用曲线C的参数方程求Q到直线l的距离的最大值与最小值的差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b是函数f(x)=x2﹣px+q(p>0,q>0)的两个不同的零点,且a,b,﹣2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于( )
A.6
B.7
C.8
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=6cos2 ![]() +
+ ![]() sinωx﹣3(ω>2)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且ABC为正三角形.
sinωx﹣3(ω>2)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且ABC为正三角形. 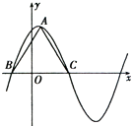
(1)求ω的值;
(2)求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0),离心率为
=1(a>b>0),离心率为 ![]() ,左准线方程是x=﹣2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB.
,左准线方程是x=﹣2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB. 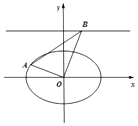
(1)求椭圆C的方程;
(2)求△AOB面积取得最小值时,线段AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两所学校全体高三年级学生在该地区八校联考中的数学成绩情况,从两校各随机抽取60名学生,将所得样本作出频数分布统计表如下: 甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 2 | 5 | 9 | 10 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 14 | 10 | 6 | 4 |
乙校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 2 | 4 | 8 | 16 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | 6 | 6 | 3 |
以抽样所得样本数据估计总体
(1)比较甲、乙两校学生的数学平均成绩的高低;
(2)若规定数学成绩不低于120分为优秀,从甲、乙两校全体高三学生中各随机抽取2人,其中数学成绩为优秀的共X人,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com