
���� ��1�����Բ�ı����̣�����ԲM��E��1��-1����F��-1��1�����㣬��Բ����x+y-2=0�ϣ����������飬������ԲM�ķ��̣�
��2�����Բ�ĵ�ֱ�ߵľ���Ϊ1���������ۣ��������ֱ�ߵķ��̣�
��3�������⣬$\overrightarrow{|{PA}|}$��Сʱ��MP��ֱ��ֱ�ߣ���ʱ|MP|=$\frac{|3+4+8|}{\sqrt{9+16}}$=3��$\overrightarrow{|{PA}|}$=$\sqrt{5}$���������ʱ$\overrightarrow{PA}•\overrightarrow{PB}$��ֵ��
��� �⣺��1����ԲM�ķ���Ϊ����x-a��2+��y-b��2=r2��r��0����
���������$\left\{\begin{array}{l}{��1-a��^{2}+��-1-b��^{2}={r}^{2}}\\{��-1-a��^{2}+��1-b��^{2}={r}^{2}}\\{a+b-2=0}\end{array}\right.$����ã�a=b=1��r=2��
������ԲM�ķ���Ϊ����x-1��2+��y-1��2=4��
��2��Բ�İ뾶Ϊ2��ֱ�߱�ԲM���صõ��ҳ�Ϊ$2\sqrt{3}$����Բ�ĵ�ֱ�ߵľ���Ϊ1��
ֱ�ߵ�б�ʲ�����ʱ��x=-2��Բ�ĵ�ֱ�ߵľ���Ϊ3�����������⣻
ֱ�ߵ�б�ʴ���ʱ���跽��Ϊy-2=k��x+2������kx-y+2k+2=0��
��Բ�ĵ�ֱ�ߵľ���Ϊ$\frac{|3k+1|}{\sqrt{{k}^{2}+1}}$=1����k=0��-$\frac{3}{4}$��
��ֱ�ߵķ���Ϊy=2��3x+4y-2=0��
��3�������⣬$\overrightarrow{|{PA}|}$��Сʱ��MP��ֱ��ֱ�ߣ���ʱ|MP|=$\frac{|3+4+8|}{\sqrt{9+16}}$=3����$\overrightarrow{|{PA}|}$=$\sqrt{5}$��
sin��APM=$\frac{2}{3}$��cos��APM=$\frac{\sqrt{5}}{3}$����cos��APB=2cos2��APM-1=$\frac{1}{9}$��
��$\overrightarrow{PA}•\overrightarrow{PB}$=$\frac{5}{9}$��
���� ���⿼��ֱ����Բ�ı����̣�����ѧ��������������������ȷ��Բ����뾶�ǹؼ��������е��⣮


 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{9}{25}$ | B�� | $\frac{4}{25}$ | C�� | $\frac{3}{10}$ | D�� | $\frac{2}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
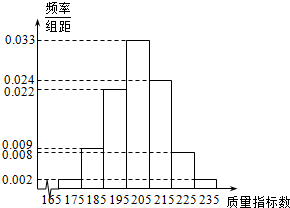
| A�� | 200 | B�� | 400 | C�� | 2000 | D�� | 4000 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��Ч | �Ǹ�Ч | ͳ�� | |
| �¿γ�ģʽ | 60 | 30 | 90 |
| ��ͳ����ģʽ | 40 | 50 | 90 |
| ͳ�� | 100 | 80 | 180 |
| P��K2�RK0�� | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | 1 | 2 | 3 | 4 | 5 |
| ���� | x | 20 | 10 | 5 | y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 50 | B�� | 77 | C�� | 78 | D�� | 306 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | g��x��=sin��2x+$\frac{5��}{12}$�� | B�� | g��x��=sin��2x+$\frac{��}{12}$�� | C�� | g��x��=sin��2x-$\frac{��}{12}$�� | D�� | g��x��=sin��2x-$\frac{5��}{12}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-6��7�� | B�� | ��-15��1�� | C�� | ��-14��2�� | D�� | ��-8��1�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com