
【题目】已知等差数列{an}满足:a3=7,a5+a7=26.{an}的前n项和为Sn . (Ⅰ)求an及Sn;
(Ⅱ)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
科目:高中数学 来源: 题型:
【题目】已知集合A={x||x﹣1|<2},B={x|x2﹣2mx+m2﹣1<0}.
(1)当m=3时,求A∩B;
(2)若A∪B=A,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 . 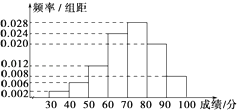
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,其中a>0,a≠1.
,其中a>0,a≠1.
(Ⅰ)若f(x)在(﹣∞,+∞)上是单调函数,求实数a,b的取值范围;
(Ⅱ)当a=2时,函数f(x)在(﹣∞,+∞)上只有一个零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定点F1(0,﹣3)、F2(0,3),动点P满足条件|PF1|+|PF2|=a+ ![]() (a>0),则点P的轨迹是( )
(a>0),则点P的轨迹是( )
A.椭圆
B.线段
C.不存在
D.椭圆或线段
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前项n和为Sn , 若对于任意的正整数n都有Sn=2an﹣3n.
(1)设bn=an+3,求证:数列{bn}是等比数列,并求出{an}的通项公式.
(2)求数列{nan}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 25 | a | b |
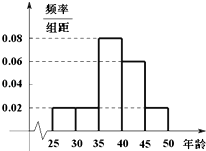
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果 ![]() ,
, ![]() 是平面
是平面 ![]() 内所有向量的一组基底,那么( )
内所有向量的一组基底,那么( )
A.若实数 ![]() ,
, ![]() ,使
,使 ![]() ,则
,则 ![]()
B.空间任一向量 ![]() 可以表示为
可以表示为 ![]() ,这里
,这里 ![]() ,
, ![]() 是实数
是实数
C.![]() ,
, ![]() 不一定在平面
不一定在平面 ![]() 内
内
D.对平面 ![]() 内任一向量
内任一向量 ![]() ,使
,使 ![]() 的实数
的实数 ![]() ,
, ![]() 有无数对
有无数对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com