
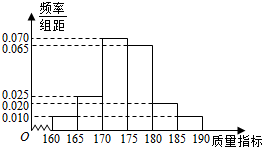
 从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.
从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.分析 (Ⅰ)根据频率分布直方图,计算数据的平均值是各小矩形底边中点与对应的频率乘积的和;
(Ⅱ)首先分别求质量指标在[180,185]的件数:0.020×5×40=4,质量指标在[185,190]的件数有:0.010×5×40=2,然后求出X=0、1、2时的概率,进而求出X的分布列及数学期望即可.
解答 解:(Ⅰ)由频率分布直方图可知,这40件样本该项质量指标的平均数$\overline{x}$=162.5×0.05+167.5×0.125+172.5×0.35+177.5×0.325+182.5×0.1+187.5×0.05=174.75cm;
(Ⅱ)由频率分布直方图可知,质量指标在[180,185]的件数:0.020×5×40=4,质量指标在[185,190]的件数有:0.010×5×40=2,∴X的可能值为:0,1,2;
P(X=0)=$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{2}{5}$,P(X=1)=$\frac{{C}_{4}^{1}{C}_{2}^{1}}{{C}_{6}^{2}}$=$\frac{8}{15}$,P(X=2)=$\frac{{C}_{2}^{2}}{{C}_{6}^{2}}$=$\frac{1}{15}$,
所以分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{2}{5}$ | $\frac{8}{15}$ | $\frac{1}{15}$ |
点评 本题主要考查了频率分布直方图的应用问题,考查了分布列以及数学期望,解答此题的关键是要熟练掌握利用频率分布直方图,计算数据的平均值的方法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,25] | B. | [4,25] | C. | [1,4] | D. | [5,24] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是减函数,有最小值0 | B. | 是增函数,有最小值0 | ||
| C. | 是减函数,有最大值0 | D. | 是增函数,有最大值0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com