9颗珍珠中有一颗是假的.且真珍珠一样重.假珍珠比真珍珠要轻．如果用一架天平至少要称( )次.就一定可以找出这颗假珍珠．A．5B．4C．2D．6 题目和参考答案——青夏教育精英家教网—

14．9颗珍珠中有一颗是假的，且真珍珠一样重，假珍珠比真珍珠要轻．如果用一架天平至少要称（　　）次，就一定可以找出这颗假珍珠．

A．

B．

C．

D．

分析将9颗珍珠分三堆，将其中两堆分别放置天平两端，如果平衡，则假珍珠在剩下一堆里；如果不平衡则假珍珠在轻的一端；再把含假珍珠的一堆中取出两颗珍珠放在天平两端，同上可找出假珍珠，故只需称两次就能找出假珍珠．

解答解析：这是工序最优化设计问题，将9颗珍珠分三堆，将其中两堆分别放置天平两端，如果平衡，则假珍珠在剩下一堆里；如果不平衡则假珍珠在轻的一端；再把含假珍珠的一堆中取出两颗珍珠放在天平两端，同上将3颗珍珠中两颗分别放置天平两端，如果平衡，则假珍珠是下一颗里；如果不平衡则假珍珠在轻的一端；可找出假珍珠，故只需称两次就能找出假珍珠．
故选：C．

点评本题考查了推理与论证，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

12．与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有共同的渐近线，且过点$（-\sqrt{3}，2\sqrt{3}）$的双曲线的标准方程是$\frac{{y}^{2}}{5}-\frac{{x}^{2}}{\frac{15}{4}}=1$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．设动点P到定点F（0，$\frac{1}{4}$）的距离与它到直线y=-$\frac{1}{4}$的距离相等，
（1）求动点P的轨迹C的方程；
（2）过（-2，0）的直线l与轨迹C交于M，N两点，又过M，N作轨迹C的切线l₁，l₂，当l₁⊥l₂时，求直线l的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

2．第4届世界杯于1950年在巴西举行，此后每4年举行一次，那么将在俄罗斯举行的2018年世界杯是第21届．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．已知椭圆C的中心在坐标原点O，右焦点$F（\sqrt{3}，0）$，M、N是椭圆C的左、右顶点，D是椭圆C上异于M、N的动点，且△MND面积的最大值为2．
（1）求椭圆C的标准方程；
（2）设直线l与椭圆C相交于A，B两点，直线OA，l，OB的斜率分别为k₁，k，k₂（其中k＞0）△OAB的面积为S，以OA，OB为直径的圆的面积分别为S₁，S₂，若k₁，k，k₂恰好构成等比数列，求$\frac{{{S_1}+{S_2}}}{S}$的最小值，并此时直线l的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

19．在长方体ABCD-A₁B₁C₁D₁中，AB=$\sqrt{2}$，BC=AA₁=1，点M在AB₁的中点，点P为对角线AC₁上的动点，点Q为底面ABCD上的动点（P，Q可以重合），则MP+PQ的最小值是$\frac{3}{4}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

6．设1＜x＜2，则$\frac{lnx}{x}$，（$\frac{lnx}{x}$）²，$\frac{ln{x}^{2}}{{x}^{2}}$的大小关系是（$\frac{lnx}{x}$）²＜$\frac{lnx}{x}$＜$\frac{ln{x}^{2}}{{x}^{2}}$（用“＜”连接）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．

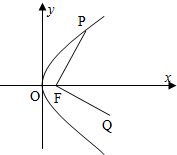如图，点P是抛物线y²=4x上动点，F为抛物线的焦点，将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$
（Ⅰ）求Q点的轨迹C的普通方程；
（Ⅱ）过F倾斜角等于$\frac{π}{4}$的直线l与曲线C交于A、B两点，求|FA|+|FB|的值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

4．

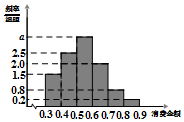某电商对10000名网购者2015年度消费情况进行统计，其消费频率分布直方图如图，则在这些网购者中，消费金额在[0.5，0.9]内的人数为（　　）

A．

2000

B．

4500

C．

6000

D．

7500

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学