
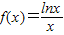
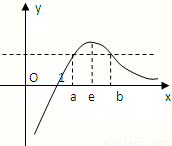
 解:(1)定义域为(0,+∞),
解:(1)定义域为(0,+∞),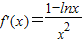 ,
, ,则x=e,
,则x=e,| x | (0,e) | e | (e,+∞) |
| f'(x) | + | - | |
| f(x) | ↗ | 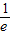 | ↘ |
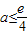 时,f(x)在[2a,4a]上单调递增,∴f(x)min=f(2a);
时,f(x)在[2a,4a]上单调递增,∴f(x)min=f(2a);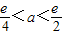 时,f(x)在[2a,e]上单调递增,f(x)在[e,4a]上单调递减,
时,f(x)在[2a,e]上单调递增,f(x)在[e,4a]上单调递减,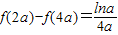 ,
,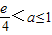 ,则f(a)-f(2a)≤0,此时
,则f(a)-f(2a)≤0,此时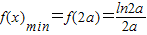 ;
;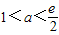 ,则f(a)-f(2a)>0,此时
,则f(a)-f(2a)>0,此时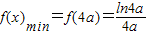 ;…(10分)
;…(10分)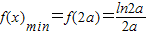 ;
;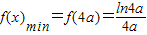 ,…(12分)
,…(12分)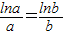 ,即ab=ba.
,即ab=ba.

科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 12 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年湖北省仙桃一中高三(上)第二次段考数学试卷(理科)(解析版) 题型:解答题


查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省枣庄市高三上学期期末检测理科数学 题型:解答题
(本题满分12分)
已知函数
(1)求函数 的极值点;
的极值点;
(2)若直线 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线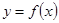 相切,求直线
相切,求直线 的方程;
的方程;
(3)设函数 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com