
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,且,
,且, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 上一点,
上一点, ![]() ,且
,且![]() 为
为![]() 的中点.
的中点.
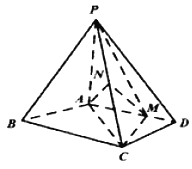
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且cosC= ![]() .
.
(1)求角B的大小;
(2)若BD为AC边上的中线,cosA= ![]() ,BD=
,BD= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,g(x)=
,g(x)= ![]() .
.
(1)当1≤x<2时,求g(x);
(2)当x∈R时,求g(x)的解析式,并画出其图象; 
(3)求方程xf[g(x)]=2g[f(x)]的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x+4y﹣4=0,是否存在斜率为1的直线l,使l被圆C截得的弦长AB为直径的圆过原点,若存在求出直线的方程l,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过原点的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() .直线
.直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.设直线
两点.设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,证明存在常数
,证明存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}为单调递减的等差数列,a1+a2+a3=21,且a1﹣1,a2﹣3,a3﹣3成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=|an|,求数列{bn}的前项n和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区上年度电价为0.8元/kWh,年用电量为akWh,本年度计划将电价降到0.55 元/kWh至0.75元/kWh之间,而用户期待电价为0.4元/kWh,下调电价后新增加的用电量与实际电价和用户期望电价的差成反比(比例系数为K),该地区的电力成本为0.3元/kWh.(注:收益=实际用电量×(实际电价﹣成本价)),示例:若实际电价为0.6元/kWh,则下调电价后新增加的用电量为 ![]() 元/kWh)
元/kWh)
(1)写出本年度电价下调后,电力部门的收益y与实际电价x的函数关系;
(2)设K=0.2a,当电价最低为多少仍可保证电力部门的收益比上一年至少增长20%?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com