
���� ��1������֪�ж����ϵ�һ�������������㹹���������Σ�����ԲC�Ľ�����x��Ĵ��߽���Բ���ҳ�Ϊ3���ɵ�a2��b2�������õ���Բ�ķ��̣�
��2���ӳ�PH����x���ڵ�Q�������õ���H����BQΪֱ����Բ�ϣ���������BQ���㣩���ɵõ�H�Ĺ켣���̣�
��� �⣺��1������ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ϵ�һ�������������㹹���������Σ�
��a=2c������
�֡߹���ԲC�Ľ�����x��Ĵ��߽���Բ���ҳ�Ϊ3��
��$\frac{2{b}^{2}}{a}$=3����
���a2=b2+c2�ã�$\left\{\begin{array}{l}a=2\\ b=\sqrt{3}\\ c=1\end{array}\right.$��
����Բ�ķ���Ϊ��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$
��2���ӳ�PH����x���ڵ�Q��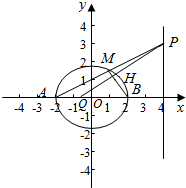
��M��x0��y0������AM�ķ���Ϊ��y=$\frac{{y}_{0}}{{x}_{0}+2}��x+2��$��
��x=4ʱ��y=$\frac{6{y}_{0}}{{x}_{0}+2}$����P������Ϊ����4��$\frac{6{y}_{0}}{{x}_{0}+2}$����
��Q��������m��0������kPQ=$\frac{\frac{6{y}_{0}}{{x}_{0}+2}}{4-m}$=$\frac{6{y}_{0}}{{��x}_{0}+2����4-m��}$��
��MB��PQ��
��kPQ•kMB=-1��
��$\frac{6{y}_{0}}{{��x}_{0}+2����4-m��}$•$\frac{{y}_{0}}{{x}_{0}+2}$=-1��
��$\frac{6{{y}_{0}}^{2}}{{{��x}_{0}}^{2}-4����4-m��}$=-1��
��$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{3}=1$����${{y}_{0}}^{2}=3-\frac{{{3x}_{0}}^{2}}{4}$��
��$\frac{6��3-\frac{{{3x}_{0}}^{2}}{4}��}{{{��x}_{0}}^{2}-4����4-m��}$=-1��
��ã�m=-$\frac{1}{2}$��
��Q��������-$\frac{1}{2}$��0����
��HQ��HB��
���H����BQΪֱ����Բ�ϣ���������BQ���㣩��
��B������Ϊ��2��0������BQ���е�����Ϊ��$\frac{3}{4}$��0����|BQ|=$\frac{5}{2}$��
��H�Ĺ켣����Ϊ��$��x-\frac{3}{4}��^{2}+{y}^{2}=\frac{25}{16}��y��0��$
���� ���⿼���֪ʶ������Բ�ļ����ʣ���Բ�ı�����ֱ������Բ��λ���ۺ�Ӧ�ã��Ѷ��е���


 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ɼ� �Ա� | �ϸ� | ���ϸ� | �ϼ� |
| ���� | 45 | 10 | |
| �� | 30 | ||
| �ϼ� | 105 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | V=S | B�� | V=2S | C�� | 2V=S | D�� | V=$\sqrt{2}$S |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
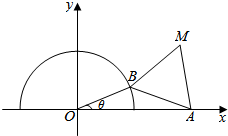 ��ͼ����֪��ԲO��x2+y2=1��y��0������A��2��0����BΪ��Բ��������һ�㣬��ABΪһ�����ȱߡ�ABM�����AOB=�ȣ�����0���ȣ��У�
��ͼ����֪��ԲO��x2+y2=1��y��0������A��2��0����BΪ��Բ��������һ�㣬��ABΪһ�����ȱߡ�ABM�����AOB=�ȣ�����0���ȣ��У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com