
分析 设|DF1|=7|F1H|=7m.D,F1到准线的距离为$\frac{7m}{e}$,$\frac{m}{e}$.利用直线的斜率,即可求出椭圆的方程.
解答 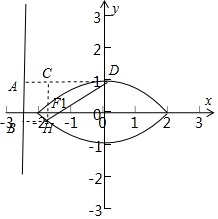 解:设|DF1|=7|F1H|=7m.D,F1到准线的距离为$\frac{7m}{e}$,$\frac{m}{e}$.
解:设|DF1|=7|F1H|=7m.D,F1到准线的距离为$\frac{7m}{e}$,$\frac{m}{e}$.
设直线DF1的倾斜角为α,则cosα=$\frac{3}{4e}$.
∵tanα=$\frac{b}{c}$,∴cosα=$\frac{c}{a}$,
∴$\frac{c}{a}$=$\frac{3}{4e}$,
∵c=$\sqrt{3}$,∴a=2.∴b=1,
∴椭圆的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
点评 本题考查椭圆的方程与性质,考查椭圆的定义,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3+(n+1)×2n | B. | 3+(n+1)×2n | C. | 1+(n+1)×2n | D. | 1+(n-1)×2n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 7816 | 6572 | 0802 | 6314 | 0702 | 4369 | 1128 | 0598 |
| 3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
| A. | 11 | B. | 02 | C. | 05 | D. | 04 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | (0,1] | C. | (0,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
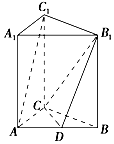 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com