
【题目】已知![]() 、
、![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的两点,
轴对称的两点,![]() 是
是![]() 的左焦点,
的左焦点,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 过点
过点![]() ,和椭圆
,和椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() ,
,![]() .点
.点![]() 坐标是
坐标是![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】为抗击“新冠肺炎”,全国各地“停课不停学”,各学校都开展了在线课堂,组织学生在线学习,并自主安排时间完成相应作业为了解学生的学习效率,某在线教育平台统计了部分高三备考学生每天完成数学作业所需的平均时间,绘制了如图所示的频率分布直方图.
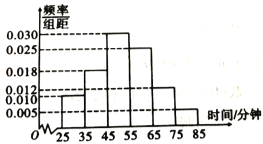
(1)如果学生在完成在线课程后每天平均自主学习时间(完成各科作业及其他自主学习)为![]() 小时,估计高三备考学生每天完成数学作业的平均时间占自主学习时间的比例(同一组中的数据用该组区间的中点值为代表)(结果精确到
小时,估计高三备考学生每天完成数学作业的平均时间占自主学习时间的比例(同一组中的数据用该组区间的中点值为代表)(结果精确到![]() );
);
(2)以统计的频率作为概率,估计一个高三备考学生每天完成数学作业的平均时间不超过![]() 分钟的概率.
分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音、短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访140位市民进行调查,其中每天玩微信超过6小时的用户称为“微信控”,否则称其为“非微信控”, 调查结果统计如下:
微信控 | 非微信控 | 合计 | |
女性 | 60 | ||
男性 | 30 | ||
合计 | 70 | 140 |
(1)根据以上数据,把表格中的数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
①是否在犯错误的概率不超过0.001的前提下认为“微信控”与“性别”有关;
②已知在被调查的女性“微信控”市民中有5位退休老人,其中2位是教师,现从这5位退休老人中随机抽取2人,求至少有1位老师的概率.
附表:![]() 其中
其中![]()
P(K2≥k) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市据实际情况主要采取以下四种扶贫方式:第一,以工代赈方式,指政府投资建设基础设施工程,组织贫困地区群众参加工程建设并获得劳务报酬,第二,整村推进方式指以贫困村为具体帮扶对象,帮扶对口到村,资金安排到村,扶贫效益到户,第三,科技扶贫方式,指组织科技人员深入贫困乡村实地指导、技术培训等传授科技知识,第四,移民搬迁方式,指对目前极少数居住在生存条件恶劣、自然资源贫乏地区的特困人口,实行自愿移民,该市为了2020年更好的完成精准扶贫各项任务,2020年初在全市贫困户(分一般贫困户和“五特”户两类)中随机抽取了5000户就目前的主要四种扶贫方式行了问卷调查,支持每种扶贫方式的结果如表:
调查的贫困户 | 支持以工代赈户数 | 支持整村推进户数 | 支持科技扶贫户数 | 支持移民搬迁户数 |
一般贫困户 | 1200 | 1600 |
| 200 |
五特户(五保户和特困户) | 100 |
|
| 100 |
已知在被调查的5000户中随机抽取一户支持整村推进的概率为0.36.
(Ⅰ)现用分层抽样的方法在所有参与调查的贫困户中抽取50户进行深入访谈,问应在支持科技扶贫户数中抽取多少户?
(Ⅱ)虽然“五特”户在全市的贫困户所占比例不大,但本次调查要有意义,其中这次调查的“五特”户户数不能低于被调查总户数的9.2%,已知![]() ,求本次调查有意义的概率是多少?
,求本次调查有意义的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业响应省政府号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了![]() 件产品作为样本,检测一项质量指标值,若该项质量指标值落在
件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表
内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表![]() 是设备改造后的样本的频数分布表.
是设备改造后的样本的频数分布表.
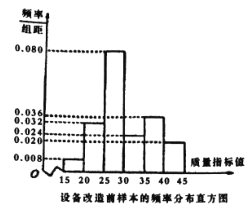
表:设备改造后样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据频率分布直方图和表 提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行登记细分,质量指标值落在![]() 内的定为一等品,每件售价
内的定为一等品,每件售价![]() 元;质量指标值落在
元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价
内的定为二等品,每件售价![]() 元;其它的合格品定为三等品,每件售价
元;其它的合格品定为三等品,每件售价![]() 元.根据表
元.根据表![]() 的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com