
分析 (1)当a=1时,f(x)=x2-2x|x-1|=$\left\{\begin{array}{l}3{x}^{2}-2x,x<1\\-{x}^{2}+2x,x≥1\end{array}\right.$,结合二次函数的图象和性质,可得f(x)的单调递增区间
(2)函数f(x)=x2-2x|x-a|=$\left\{\begin{array}{l}3{x}^{2}-2ax,x<a\\-{x}^{2}+2ax,x≥a\end{array}\right.$,结合二次函数的图象和性质分类讨论满足M(a)-m(a)≤4的a的取值范围,最后综合讨论结果,可得答案.
解答 解:(1)当a=1时,f(x)=x2-2x|x-1|=$\left\{\begin{array}{l}3{x}^{2}-2x,x<1\\-{x}^{2}+2x,x≥1\end{array}\right.$,
∵y=3x2-2x的图象是开口朝上且以x=$\frac{1}{3}$为对称轴的抛物线,
∴当x<1时,函数f(x)在[$\frac{1}{3}$,1)为递增;
y=-x2+2x的图象是开口朝下且以x=1为对称轴的抛物线,
∴当x≥1时,函数f(x)为减函数,
综上所述:a=1时,求f(x)的单调递增区间为[$\frac{1}{3}$,1);
(2)函数f(x)=x2-2x|x-a|=$\left\{\begin{array}{l}3{x}^{2}-2ax,x<a\\-{x}^{2}+2ax,x≥a\end{array}\right.$,
当-1≤a≤0时,
当x<a时,y=3x2-2ax的图象是开口朝上且以x=$\frac{1}{3}$a≥a为对称轴的抛物线,函数f(x)为减函数;
当x≥a时,y=-x2+2ax的图象是开口朝下且以x=a为对称轴的抛物线,函数f(x)为减函数;
故f(x)在x∈[-1,1]上的最大值为M(a)=f(-1)=3+2a,最小值为m(a)=f(1)=-1+2a,
此时M(a)-m(a)=4≤4恒成立,
当a>0时,
当x<a时,y=3x2-2ax的图象是开口朝上且以x=$\frac{1}{3}$a<a为对称轴的抛物线,函数f(x)在[-1,$\frac{1}{3}$a]上为减函数,在[$\frac{1}{3}$a,a]为增函数;
当x≥a时,y=-x2+2ax的图象是开口朝下且以x=a为对称轴的抛物线,函数f(x)为减函数;
由f($\frac{1}{3}$a)=$-\frac{1}{3}$a2,f(1)=-1+2a,
若0<a≤2$\sqrt{3}$-3,f(1)≤f($\frac{1}{3}$a),
故f(x)在x∈[-1,1]上的最大值为M(a)=f(-1)=3+2a,最小值为m(a)=f(1)=-1+2a,
此时M(a)-m(a)=4≤4恒成立,
若2$\sqrt{3}$-3<a≤1,f(1)>f($\frac{1}{3}$a),
故f(x)在x∈[-1,1]上的最大值为M(a)=f(-1)=3+2a,最小值为m(a)=f($\frac{1}{3}$a)=$-\frac{1}{3}$a2,
此时M(a)-m(a)≤4无解,
综上所述,-1≤a≤2$\sqrt{3}$-3
点评 本题考查的知识点是分段函数的应用,二次函数的图象和性质,分类讨论思想,难度中档.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
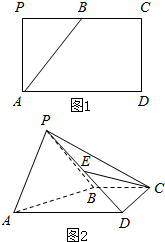 如图1,矩形APCD中,AD=2AP,B为PC的中点,将△APB折沿AB折起,使得PD=PC,如图2.
如图1,矩形APCD中,AD=2AP,B为PC的中点,将△APB折沿AB折起,使得PD=PC,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
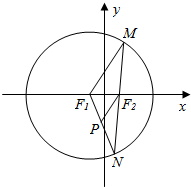 已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.
已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+2 | B. | $\sqrt{3}$-1 | C. | -$\sqrt{3}$+1 | D. | -$\sqrt{3}$+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com