
【题目】已知函数![]() ,
,![]() ,对于不相等的实数
,对于不相等的实数![]() 、
、![]() ,设
,设![]() ,
,![]() ,现有如下命题:
,现有如下命题:
①对于任意不相等的实数![]() 、
、![]() ,都有
,都有![]() ;
;
②对于任意的![]() 及任意不相等的实数
及任意不相等的实数![]() 、
、![]() ,都有
,都有![]() ;
;
③对于任意的![]() ,存在不相等的实数
,存在不相等的实数![]() 、
、![]() ,使得
,使得![]() ;
;
④对于任意的![]() ,存在不相等的实数
,存在不相等的实数![]() 、
、![]() ,使得
,使得![]() ;
;
其中所有的真命题的序号是_______.
【答案】①④
【解析】
①根据函数单调性的定义来判断是否正确. ②通过举反例来判断是否正确. ③通过构造函数![]() ,利用导数研究
,利用导数研究![]() 的单调性来判断是否正确. ④通过构造函数
的单调性来判断是否正确. ④通过构造函数![]() ,利用导数研究
,利用导数研究![]() 的单调性来判断是否正确.
的单调性来判断是否正确.
对于①,由于![]() 在
在![]() 上单调递增,根据单调性的定义可知,对于任意不相等的实数
上单调递增,根据单调性的定义可知,对于任意不相等的实数![]() 、
、![]() ,都有
,都有![]() ,故①是真命题.
,故①是真命题.
对于②,当![]() 时,
时,![]() ,则
,则![]() ,所以②是假命题.
,所以②是假命题.
对于③,若![]() ,则
,则![]() ,即
,即![]() ,即
,即![]() ,令
,令![]() ,由于
,由于![]() ,所以
,所以![]() 不是单调函数.令
不是单调函数.令![]() ,得
,得![]() .令
.令![]() ,则由
,则由![]() 解得
解得![]() ,所以
,所以![]() 在
在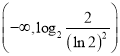 上递减,在
上递减,在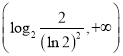 上递增,当
上递增,当![]() 时
时![]() 取得极小值也即是最小值,所以
取得极小值也即是最小值,所以![]() 不满足对任意实数
不满足对任意实数![]() 成立.所以③错误.
成立.所以③错误.
对于④,若![]() ,则
,则![]() ,即
,即![]() ,即
,即![]() ,令
,令![]() ,由于
,由于![]() ,所以
,所以![]() 不是单调函数.令
不是单调函数.令![]() ,得
,得![]() .令
.令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递减,值域为
上单调递减,值域为![]() ,所以
,所以![]() 满足对任意实数
满足对任意实数![]() 成立.所以对于任意的
成立.所以对于任意的![]() ,存在不相等的实数
,存在不相等的实数![]() 、
、![]() ,使得
,使得![]() ,所以④为真命题.
,所以④为真命题.
故答案为:①④


科目:高中数学 来源: 题型:
【题目】![]() 年诺贝尔生理学或医学奖获得者威廉·凯林(WilliamG.KaelinJr)在研究肾癌的
年诺贝尔生理学或医学奖获得者威廉·凯林(WilliamG.KaelinJr)在研究肾癌的![]() 抑制剂过程中使用的输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后
抑制剂过程中使用的输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后![]() 分钟,瓶内液面与进气管的距离为
分钟,瓶内液面与进气管的距离为![]() 厘米,已知当
厘米,已知当![]() 时,
时,![]() .如果瓶内的药液恰好
.如果瓶内的药液恰好![]() 分钟滴完.则函数
分钟滴完.则函数![]() 的图像为( )
的图像为( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.
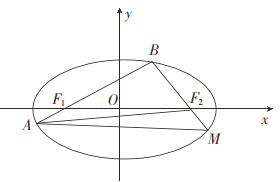
(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,如图2,点
折起,如图2,点![]() 是棱
是棱![]() 上的点.
上的点.
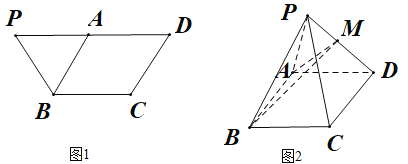
(1)若![]() 为
为![]() 的中点,证明:平面
的中点,证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,试确定
,试确定![]() 的位置,使二面角
的位置,使二面角![]() 的余弦值等于
的余弦值等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已定义![]() ,已知函数
,已知函数![]() 的定义域都是
的定义域都是![]() ,则下列四个命题中为真命题的是_________.(写出所有真命题的序号)
,则下列四个命题中为真命题的是_________.(写出所有真命题的序号)
① 若![]() 都是奇函数,则函数
都是奇函数,则函数![]() 为奇函数.
为奇函数.
② 若![]() 都是偶函数,则函数
都是偶函数,则函数![]() 为偶函数.
为偶函数.
③ 若![]() 都是增函数,则函数
都是增函数,则函数![]() 为增函数.
为增函数.
④ 若![]() 都是减函数,则函数
都是减函数,则函数![]() 为减函数.
为减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]()
![]() 为公海与领海的分界线,一艘巡逻艇在原点
为公海与领海的分界线,一艘巡逻艇在原点![]() 处发现了北偏东
处发现了北偏东![]() 海面上
海面上![]() 处有一艘走私船,走私船正向停泊在公海上接应的走私海轮
处有一艘走私船,走私船正向停泊在公海上接应的走私海轮![]() 航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.
航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.
(1)如果走私船和巡逻船相距6海里,求走私船能被截获的点的轨迹;
(2)若![]() 与公海的最近距离20海里,要保证在领海内捕获走私船,则
与公海的最近距离20海里,要保证在领海内捕获走私船,则![]() ,
,![]() 之间的最远距离是多少海里?
之间的最远距离是多少海里?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com