
【题目】设![]() 方程
方程![]() 有两个不等的负根,
有两个不等的负根, ![]() 方程
方程![]() 无实根,若“
无实根,若“![]() ”为真,“
”为真,“![]() ”为假,求实数
”为假,求实数![]() 的取值范围.
的取值范围.
【答案】(1,2]∪[3,+∞)
【解析】试题分析:本题考查逻辑联接词,由“![]() 或
或![]() ”为真,“
”为真,“![]() 且
且![]() ”为假可知,“
”为假可知,“![]() 真
真![]() 假”或“
假”或“![]() 假
假![]() 真”,先求命题
真”,先求命题![]() 为真命题时实数
为真命题时实数![]() 的取值范围,从而得到
的取值范围,从而得到![]() 为假命题时
为假命题时![]() 的取值范围,同样先求命题
的取值范围,同样先求命题![]() 为真命题时
为真命题时![]() 的取值范围,再求
的取值范围,再求![]() 为假命题时
为假命题时![]() 的取值范围,然后求“
的取值范围,然后求“![]() 真
真![]() 假”时
假”时![]() 的范围,求“
的范围,求“![]() 假
假![]() 真”时
真”时![]() 的范围,最后取两部分范围的并集.
的范围,最后取两部分范围的并集.
试题解析:若方程![]() 有两个不等的负根,则
有两个不等的负根,则![]() ,解得
,解得![]() .
.
即![]() ………………2分
………………2分
若方程![]() 无实根,
无实根,
则![]() ,
,
解得: ![]() ,即
,即![]() .…………4分
.…………4分
因“![]() ”为真,所以
”为真,所以![]() 至少有一为真,又“
至少有一为真,又“![]() ”为假,所以
”为假,所以![]() 至少有一为假,
至少有一为假,
因此, ![]() 两命题应一真一假,即
两命题应一真一假,即![]() 为真,
为真, ![]() 为假或
为假或![]() 为假,
为假, ![]() 为真.……6分
为真.……6分
∴![]() 或
或![]() .
.
解得: ![]() 或
或![]() .…………………………10分
.…………………………10分


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的值;(2)求
的值;(2)求![]() 的单调区间;
的单调区间;
(3)设![]() (其中
(其中![]() 为
为![]() 的导函数)。证明:对任意
的导函数)。证明:对任意![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学参加科普知识竞赛,需回答3个问题,竞赛规则规定:答对第一、二、三问题分别得100分、100分、200分,答错得零分,假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响.
(1)求这名同学得300分的概率;
(2)求这名同学至少得300分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于空间直角坐标系![]() 中的一点
中的一点![]() ,有下列说法:
,有下列说法:
①点![]() 到坐标原点的距离为
到坐标原点的距离为![]() ;
;
②![]() 的中点坐标为
的中点坐标为![]() ;
;
③点![]() 关于
关于![]() 轴对称的点的坐标为
轴对称的点的坐标为![]() ;
;
④点![]() 关于坐标原点对称的点的坐标为
关于坐标原点对称的点的坐标为![]() ;
;
⑤点![]() 关于坐标平面
关于坐标平面![]() 对称的点的坐标为
对称的点的坐标为![]() .
.
其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在遂宁市中央商务区的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、2只白色的乒乓球(其体积,质地完全相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得统一颜色的3个球,摊主送个摸球者10元钱;若摸得非同一颜色的3个球。摸球者付给摊主2元钱。
(1)摸出的3个球中至少有1个白球的概率是多少?
(2)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究性学习中,关于三角形与三角函数知识的应用(约定三内角![]() 所对的边分别是
所对的边分别是![]() )得出如下一些结论:
)得出如下一些结论:
(1)若![]() 是钝角三角形,则
是钝角三角形,则![]() ;
;
(2)若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
(3)在三角形![]() 中,若
中,若![]() ,则
,则![]()
(4)在![]() 中,若
中,若![]() ,则
,则![]()
其中错误命题的个数是 ( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过点![]() ,则
,则
(1)若直线l与x轴、y轴的正半轴分别交于A、B两点,且△OAB的面积为4,求直线l的方程;
(2)若直线l与原点距离为2,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足![]() ,
,
(1)求数列{an}的通项公式;
(2)求证:数列{an}中的任意三项不可能成等差数列;
(3)设![]() ,Tn为{bn}的前n项和,求证
,Tn为{bn}的前n项和,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知一个八面体各棱长均为1,四边形ABCD为正方形,则下列命题中不正确的是
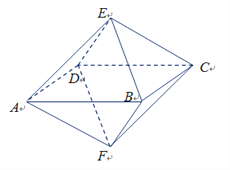
A. 不平行的两条棱所在直线所成的角为![]() 或
或![]() B. 四边形AECF为正方形
B. 四边形AECF为正方形
C. 点A到平面BCE的距离为![]() D. 该八面体的顶点在同一个球面上
D. 该八面体的顶点在同一个球面上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com