
【题目】在各项均为正数的等比数列![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足
满足![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和. 设
项和. 设![]() ,当
,当![]() 最大时,求
最大时,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]()
【解析】
(Ⅰ)根据等比数列的通项公式,结合等差中项的定义列式,得2q4=2 q2+3×q3,解之得q=2(舍负),由此算出a1的值,即可得到数列{an}的通项公式;
(Ⅱ)根据对数的运算法则,结合an=2n﹣2算出bn=2n,从而得到{bn}构成等差数列,得出{bn}的前n项和Sn=n2-n,由此化简cn得cn=![]() .利用
.利用![]() 与0的大小,得到n≤5时c6>c5>…>c1,当n=6时,c6=c7;当n≥7时,c7>c8>…>cn,由此即可得到当cn最大时,求n的值为6或7.
与0的大小,得到n≤5时c6>c5>…>c1,当n=6时,c6=c7;当n≥7时,c7>c8>…>cn,由此即可得到当cn最大时,求n的值为6或7.
(Ⅰ)设等比数列![]() 的公比为
的公比为![]() ,则
,则![]()
由![]() 得
得![]() ,
,
依题意,![]()
∴![]() 即
即![]()
解得![]() 或
或![]() (舍)
(舍)
所以![]() 的通项公式为
的通项公式为![]()
(Ⅱ)![]()
∵![]()
∴![]() 成等差数列
成等差数列
∴![]()
(法一)![]()
∵![]()
当![]() 时,
时,![]() 即
即![]()
当![]() 时,
时,![]() 即
即![]()
当![]() 时,
时,![]() 即
即![]()
∴![]()
∴ 当![]() 最大时,
最大时,![]() 或
或![]()
(法二)由![]() 得
得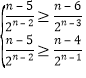
解得![]()
∴ 当![]() 最大时,
最大时,![]() 或
或![]()


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱垂直于底面,
中,侧棱垂直于底面,![]() ,
, ![]() 为
为![]() 的中点,过
的中点,过![]() 的平面与
的平面与![]() 交于点
交于点![]() .
.

(1)求证:点![]() 为
为![]() 的中点;
的中点;
(2)四边形![]() 是什么平面图形?说明理由,并求其面积.
是什么平面图形?说明理由,并求其面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系xOy中,圆C的参数方程为 ![]() (θ为参数,r>0).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(θ为参数,r>0).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 ![]() ρsin(θ+
ρsin(θ+ ![]() )+1=0.
)+1=0.
(1)求圆C的圆心的极坐标;
(2)当圆C与直线l有公共点时,求r的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)=ax2+bx+c(a,b∈R)满足条件:①当x∈R时,f(x)的最大值为0,且f(x﹣1)=f(3﹣x)成立;②二次函数f(x)的图象与直线y=﹣2交于A、B两点,且|AB|=4
(Ⅰ)求f(x)的解析式;
(Ⅱ)求最小的实数n(n<﹣1),使得存在实数t,只要当x∈[n,﹣1]时,就有f(x+t)≥2x成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若lg(3x)+lg y=lg(x+y+1),则xy的最小值为( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
先根据对称的运算性质化简得到3xy=x+y+1,再根据基本不等式即可求出答案.
∵lg(3x)+lgy=lg(3xy)=lg(x+y+1),x>0,y>0,
∴3xy=x+y+1,
∴3xy≥3![]() ,当且仅当x=y=1时取等号,
,当且仅当x=y=1时取等号,
即xy≥1,
∴xy的最小值是1,
故选:A
【点睛】
在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误
【题型】单选题
【结束】
12
【题目】已知两定点![]() ,如果动点
,如果动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹所包围的图形的面积等于( )
的轨迹所包围的图形的面积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图的程序图的算法思路中是一种古老而有效的算法﹣﹣辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )
A.0
B.2
C.3
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2﹣alnx,a∈R.
(1)讨论函数f(x)的单调性;
(2)当a>0时,若f(x)的最小值为1,求a的值;
(3)设g(x)=f(x)﹣2x,若g(x)在[![]() ,
, ![]() ]有两个极值点x1 , x2(x1<x2),证明:g(x1)﹣g(x2)的取值范围.
]有两个极值点x1 , x2(x1<x2),证明:g(x1)﹣g(x2)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com