
°æƒø°ø»ÁÕº£¨”ŒøÕ¥”ƒ≥¬√”Œæ∞«¯µƒæ∞µ„![]() ¥¶œ¬…œ÷¡
¥¶œ¬…œ÷¡![]() ¥¶”–¡Ω÷÷¬∑æ∂£Æ“ª÷÷ «¥”
¥¶”–¡Ω÷÷¬∑æ∂£Æ“ª÷÷ «¥”![]() —ÿ÷±œþ≤Ω––µΩ
—ÿ÷±œþ≤Ω––µΩ![]() £¨¡Ì“ª÷÷ «œ»¥”
£¨¡Ì“ª÷÷ «œ»¥”![]() —ÿÀ˜µ¿≥À¿¬≥µµΩ
—ÿÀ˜µ¿≥À¿¬≥µµΩ![]() £¨»ª∫Û¥”
£¨»ª∫Û¥”![]() —ÿ÷±œþ≤Ω––µΩ
—ÿ÷±œþ≤Ω––µΩ![]() £Æœ÷”–º◊°¢““¡ΩŒª”ŒøÕ¥”
£Æœ÷”–º◊°¢““¡ΩŒª”ŒøÕ¥”![]() ¥¶œ¬…Ω£¨º◊—ÿ
¥¶œ¬…Ω£¨º◊—ÿ![]() ‘»ÀŸ≤Ω––£¨ÀŸ∂»Œ™
‘»ÀŸ≤Ω––£¨ÀŸ∂»Œ™![]() £Æ‘⁄º◊≥ˆ∑¢
£Æ‘⁄º◊≥ˆ∑¢![]() ∫Û£¨““¥”
∫Û£¨““¥”![]() ≥À¿¬≥µµΩ
≥À¿¬≥µµΩ![]() £¨‘⁄
£¨‘⁄![]() ¥¶Õ£¡Ù
¥¶Õ£¡Ù![]() ∫Û£¨‘Ÿ¥”
∫Û£¨‘Ÿ¥”![]() ‘»ÀŸ≤Ω––µΩ
‘»ÀŸ≤Ω––µΩ![]() £¨ºŸ…Ë¿¬≥µ‘»ÀŸ÷±œþ‘À∂صƒÀŸ∂»Œ™
£¨ºŸ…Ë¿¬≥µ‘»ÀŸ÷±œþ‘À∂صƒÀŸ∂»Œ™![]() £¨…Ω¬∑
£¨…Ω¬∑![]() ≥§Œ™1260
≥§Œ™1260![]() £¨æ≠≤‚¡ø
£¨æ≠≤‚¡ø![]() £¨
£¨![]() £Æ
£Æ
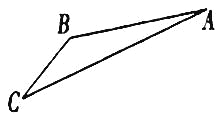
£®1£©«ÛÀ˜µ¿![]() µƒ≥§£ª
µƒ≥§£ª
£®2£©Œ £∫““≥ˆ∑¢∂ý…Ÿ![]() ∫Û£¨““‘⁄¿¬≥µ…œ”κ◊µƒæý¿Î◊Ó∂ãø
∫Û£¨““‘⁄¿¬≥µ…œ”κ◊µƒæý¿Î◊Ó∂ãø
£®3£©Œ™ π¡ΩŒª”ŒøÕ‘⁄![]() ¥¶ª•œýµ»¥˝µƒ ±º‰≤ª≥¨π˝
¥¶ª•œýµ»¥˝µƒ ±º‰≤ª≥¨π˝![]() £¨““≤Ω––µƒÀŸ∂»”¶øÿ÷∆‘⁄ ≤√¥∑∂Œßƒ⁄£ø
£¨““≤Ω––µƒÀŸ∂»”¶øÿ÷∆‘⁄ ≤√¥∑∂Œßƒ⁄£ø
°æ¥∞∏°ø£®1£©![]() m £®2£©
m £®2£©![]() £®3£©
£®3£©![]() £®µ•Œª£∫m/min£©
£®µ•Œª£∫m/min£©
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©∏˘æð¡ΩΩ«∫Õπ´ Ω«Ûµ√![]() £¨‘Ÿ∏˘æð’˝œ“∂®¿Ìº¥ø…«Ûµ√
£¨‘Ÿ∏˘æð’˝œ“∂®¿Ìº¥ø…«Ûµ√![]() µƒ≥§£ª£®2£©ºŸ…Ë““≥ˆ∑¢
µƒ≥§£ª£®2£©ºŸ…Ë““≥ˆ∑¢![]() ∫Û£¨º◊°¢““¡Ω”ŒøÕæý¿ÎŒ™
∫Û£¨º◊°¢““¡Ω”ŒøÕæý¿ÎŒ™![]() £¨∑÷±±Ì æ≥ˆº◊°¢““∂˛»À––◊þµƒæý¿Î£¨∏˘æð”ýœ“∂®¿ÌΩ®¡¢
£¨∑÷±±Ì æ≥ˆº◊°¢““∂˛»À––◊þµƒæý¿Î£¨∏˘æð”ýœ“∂®¿ÌΩ®¡¢![]() µƒ∂˛¥Œ∫Ø ˝πÿœµ£¨«Û≥ˆ πµ√º◊““∂˛»Àæý¿Î◊Ó∂à ±
µƒ∂˛¥Œ∫Ø ˝πÿœµ£¨«Û≥ˆ πµ√º◊““∂˛»Àæý¿Î◊Ó∂à ±![]() µƒ÷µ£ª£®3£©∏˘æð’˝œ“∂®¿Ì«Ûµ√
µƒ÷µ£ª£®3£©∏˘æð’˝œ“∂®¿Ì«Ûµ√![]() ,““¥”
,““¥”![]() ≥ˆ∑¢ ±£¨º◊“—◊þ¡À
≥ˆ∑¢ ±£¨º◊“—◊þ¡À![]()
![]() £¨ªπ–Ë◊þ
£¨ªπ–Ë◊þ![]()
![]() ≤≈ƒÐµΩ¥Ô
≤≈ƒÐµΩ¥Ô![]() ,…Ë““≤Ω––µƒÀŸ∂»Œ™
,…Ë““≤Ω––µƒÀŸ∂»Œ™![]() £¨”…“‚µ√
£¨”…“‚µ√![]() ,Ω‚≤ªµ» Ωº¥ø…«Ûµ√““≤Ω––ÀŸ∂»µƒ∑∂Œß.
,Ω‚≤ªµ» Ωº¥ø…«Ûµ√““≤Ω––ÀŸ∂»µƒ∑∂Œß.
‘Ã‚Ω‚Œˆ£∫£®1£©‘⁄![]() ÷–£¨“ÚŒ™
÷–£¨“ÚŒ™![]() £¨
£¨![]() £¨
£¨
À˘“‘![]() £¨
£¨![]() £¨
£¨
¥”∂¯![]()
![]()
![]() £Æ
£Æ
”…’˝œ“∂®¿Ì![]() £¨µ√
£¨µ√![]() £®
£®![]() £©£Æ
£©£Æ
£®2£©ºŸ…Ë““≥ˆ∑¢![]() ∫Û£¨º◊°¢““¡Ω”ŒøÕæý¿ÎŒ™
∫Û£¨º◊°¢““¡Ω”ŒøÕæý¿ÎŒ™![]() £¨¥À ±£¨º◊––◊þ¡À
£¨¥À ±£¨º◊––◊þ¡À![]() £¨““æý¿Î
£¨““æý¿Î![]() ¥¶
¥¶![]()
![]() £¨
£¨
À˘“‘”…”ýœ“∂®¿Ìµ√![]()
![]() £¨
£¨
”…”⁄![]() £¨º¥
£¨º¥![]() £¨
£¨
π µ±![]() ±£¨º◊°¢““¡Ω”ŒøÕæý¿Î◊Ó∂ãÆ
±£¨º◊°¢““¡Ω”ŒøÕæý¿Î◊Ó∂ãÆ
£®3£©”…’˝œ“∂®¿Ì![]() £¨
£¨
µ√![]() £®
£®![]() £©£Æ
£©£Æ
““¥”![]() ≥ˆ∑¢ ±£¨º◊“—◊þ¡À
≥ˆ∑¢ ±£¨º◊“—◊þ¡À![]() £®
£®![]() £©£¨ªπ–Ë◊þ710
£©£¨ªπ–Ë◊þ710![]() ≤≈ƒÐµΩ¥Ô
≤≈ƒÐµΩ¥Ô![]() £Æ
£Æ
…Ë““≤Ω––µƒÀŸ∂»Œ™![]() £¨”…“‚µ√
£¨”…“‚µ√![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
À˘“‘Œ™ π¡ΩŒª”ŒøÕ‘⁄![]() ¥¶ª•œýµ»¥˝µƒ ±º‰≤ª≥¨π˝
¥¶ª•œýµ»¥˝µƒ ±º‰≤ª≥¨π˝![]() £¨““≤Ω––µƒÀŸ∂»”¶øÿ÷∆‘⁄
£¨““≤Ω––µƒÀŸ∂»”¶øÿ÷∆‘⁄![]() £®µ•Œª£∫
£®µ•Œª£∫![]() £©∑∂Œßƒ⁄£Æ
£©∑∂Œßƒ⁄£Æ


 ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏
ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏ –°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
–°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂®“‘⁄![]() …œµƒ∆Ê∫Ø ˝
…œµƒ∆Ê∫Ø ˝![]() ¬˙◊„
¬˙◊„![]() £¨«“‘⁄
£¨«“‘⁄![]() …œ «ºı∫Ø ˝£¨
…œ «ºı∫Ø ˝£¨ ![]() £¨
£¨ ![]() «»ÒΩ«»˝Ω«–Œµƒ¡Ω∏ˆƒ⁄Ω«£¨‘Ú
«»ÒΩ«»˝Ω«–Œµƒ¡Ω∏ˆƒ⁄Ω«£¨‘Ú![]() ”Î
”Î![]() µƒ¥Û–°πÿœµ «£® £©
µƒ¥Û–°πÿœµ «£® £©
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº« ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() £¨»Ù¥Ê‘⁄ µ ˝
£¨»Ù¥Ê‘⁄ µ ˝![]() £¨ πµ√∂‘»Œ“‚µƒ
£¨ πµ√∂‘»Œ“‚µƒ![]() £¨∂º”–
£¨∂º”–![]() £¨‘Ú≥∆ ˝¡–
£¨‘Ú≥∆ ˝¡–![]() Œ™°∞∫Õ”–ΩÁ ˝¡–°±. œ¬¡–√¸Ã‚’˝»∑µƒ «( )
Œ™°∞∫Õ”–ΩÁ ˝¡–°±. œ¬¡–√¸Ã‚’˝»∑µƒ «( )
A. »Ù![]() «µ»≤Ó ˝¡–£¨«“ ◊œÓ
«µ»≤Ó ˝¡–£¨«“ ◊œÓ![]() £¨‘Ú
£¨‘Ú![]() «°∞∫Õ”–ΩÁ ˝¡–°±
«°∞∫Õ”–ΩÁ ˝¡–°±
B. »Ù![]() «µ»≤Ó ˝¡–£¨«“π´≤Ó
«µ»≤Ó ˝¡–£¨«“π´≤Ó![]() £¨‘Ú
£¨‘Ú![]() «°∞∫Õ”–ΩÁ ˝¡–°±
«°∞∫Õ”–ΩÁ ˝¡–°±
C. »Ù![]() «µ»±» ˝¡–£¨«“π´±»
«µ»±» ˝¡–£¨«“π´±»![]() £¨‘Ú
£¨‘Ú![]() «°∞∫Õ”–ΩÁ ˝¡–°±
«°∞∫Õ”–ΩÁ ˝¡–°±
D. »Ù![]() «µ»±» ˝¡–£¨«“
«µ»±» ˝¡–£¨«“![]() «°∞∫Õ”–ΩÁ ˝¡–°±£¨‘Ú
«°∞∫Õ”–ΩÁ ˝¡–°±£¨‘Ú![]() µƒπ´±»
µƒπ´±»![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë ![]() «∂®“‘⁄
«∂®“‘⁄ ![]() …œµƒ∆Ê∫Ø ˝£¨«“∆‰ÕºœÛπÿ”⁄÷±œþ
…œµƒ∆Ê∫Ø ˝£¨«“∆‰ÕºœÛπÿ”⁄÷±œþ ![]() ∂‘≥∆£¨µ±
∂‘≥∆£¨µ± ![]() ±£¨
±£¨ ![]() £¨‘Ú
£¨‘Ú ![]() µƒ÷µŒ™( )
µƒ÷µŒ™( )
A.![]()
B.0
C.1
D.≤ªƒÐ»∑∂®
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤ ![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™ ![]() £¨∆‰÷–◊ÛΩπµ„Œ™
£¨∆‰÷–◊ÛΩπµ„Œ™ ![]() .
.
£®1£©«ÛÕ÷‘≤ ![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©π˝ ![]() µƒ÷±œþ
µƒ÷±œþ ![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤ ![]() œýΩª”⁄
œýΩª”⁄ ![]() ¡Ωµ„£¨»Ù
¡Ωµ„£¨»Ù ![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™ ![]() £¨«Û“‘
£¨«Û“‘ ![]() Œ™‘≤–ƒ«“”Î÷±œþ
Œ™‘≤–ƒ«“”Î÷±œþ ![]() œý«–µƒ‘≤µƒ∑Ω≥Ã.
œý«–µƒ‘≤µƒ∑Ω≥Ã.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄º´◊¯±Íœµœ¬£¨“—÷™÷±œþ ![]() (
( ![]() )∫Õ‘≤
)∫Õ‘≤ ![]() .‘≤
.‘≤ ![]() ”Î÷±œþ
”Î÷±œþ ![]() µƒΩªµ„Œ™
µƒΩªµ„Œ™ ![]() .
.
£®1£©«Û‘≤ ![]() µƒ÷±Ω«◊¯±Í∑Ω≥ã¨≤¢–¥≥ˆ‘≤
µƒ÷±Ω«◊¯±Í∑Ω≥ã¨≤¢–¥≥ˆ‘≤ ![]() µƒ‘≤–ƒ”Î∞Îæ∂.
µƒ‘≤–ƒ”Î∞Îæ∂.
£®2£©«Û ![]() µƒ√ʪ˝.
µƒ√ʪ˝.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº◊°¢““¡Ω¥¨ ªœÚ“ª∏ˆ≤ªƒÐÕ¨ ±Õ£≤¥¡ΩÀ“¥¨µƒ¬ÎÕ∑£¨À¸√«‘⁄“ªÃÏ∂˛ ÆÀƒ–° ±ƒ⁄µΩ¥Ô∏√¬ÎÕ∑µƒ ±øà «µ»ø…ƒÐµƒ£Æ»Áπ˚º◊¥¨Õ£≤¥ ±º‰Œ™1–° ±£¨““¥¨Õ£≤¥ ±º‰Œ™2–° ±£¨«ÛÀ¸√«÷–µƒ»Œ“‚“ªÀ“∂º≤ª–Ë“™µ»¥˝¬ÎÕ∑ø’≥ˆµƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡ÀΩ‚…ŸƒÍ∂˘Õصƒ∑ ≈÷ «∑Ò”Î≥£∫»ÃºÀ·“˚¡œ”–πÿ£¨œ÷∂‘30√˚¡˘ƒÍº∂—ß…˙Ω¯––¡ÀŒ æ̵˜≤È£¨µ√µΩ»Áœ¬¡–¡™±Ì£®∆Ωæ˘√øÃÏ∫»500ml“‘…œŒ™≥£∫»£¨ÃÂ÷ÿ≥¨π˝50kgŒ™∑ ≈÷£©£∫
≥£∫» | ≤ª≥£∫» | ∫œº∆ | |
∑ ≈÷ | 2 | ||
≤ª∑ ≈÷ | 18 | ||
∫œº∆ | 30 |
“—÷™‘⁄»´≤ø30»À÷–Àʪ˙≥È»°1»À£¨≥ȵΩ∑ ≈÷µƒ—ß…˙µƒ∏≈¬ Œ™ ![]() £Æ
£Æ
£®1£©«ÎΩ´…œ√ʵƒ¡–¡™±Ì≤π≥‰ÕÍ’˚£ª
£®2£© «∑Ò”–99.5%µƒ∞—Œ’»œŒ™∑ ≈÷”Î≥£∫»ÃºÀ·“˚¡œ”–πÿ£øÀµ√˜ƒ„µƒ¿Ì”…£ª
£®3£©œ÷¥”≥£∫»ÃºÀ·“˚¡œ«“∑ ≈÷µƒ—ß…˙÷–£®2√˚≈Æ…˙£©£¨≥È»°2»À≤Œº”µÁ ”Ω⁄ƒø£¨‘Ú’˝∫√≥ÈµΩ“ªƒ–“ª≈Ƶƒ∏≈¬ «∂ý…Ÿ
P£®K2°ðk£© | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
£®≤Œøºπ´ Ω£∫K2= ![]() £¨∆‰÷–n=a+b+c+d£©
£¨∆‰÷–n=a+b+c+d£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµxoy÷–£¨µ„ ![]() £¨‘≤F2£∫x2+y2©Å2
£¨‘≤F2£∫x2+y2©Å2 ![]() x©Å13=0£¨“‘∂ص„PŒ™‘≤–ƒµƒ‘≤æ≠π˝µ„F1 £¨ «“‘≤P”Α≤F2ƒ⁄«–£Æ
x©Å13=0£¨“‘∂ص„PŒ™‘≤–ƒµƒ‘≤æ≠π˝µ„F1 £¨ «“‘≤P”Α≤F2ƒ⁄«–£Æ
£®1£©«Û∂ص„µƒπϺ£µƒ∑Ω≥ãª
£®2£©»Ù÷±œþlπ˝µ„£®1£¨0£©£¨«“”Ϋ˙œþEΩª”⁄A£¨B¡Ωµ„£¨‘Ú‘⁄x÷·…œ «∑ҥʑ⁄“ªµ„D£®t£¨0£©£®t°Ÿ0£©£¨ πµ√x÷·∆Ω∑÷°œADB£ø»Ù¥Ê‘⁄£¨«Û≥ˆtµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com