
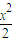 +y2=1�ϣ�����Q�Ƕ�ԲC2��x2+y2=r2��1��r��2����һ�㣮
+y2=1�ϣ�����Q�Ƕ�ԲC2��x2+y2=r2��1��r��2����һ�㣮 ����C��x2��y2�����F��1��0���ľ���ɵȲ����У��߶�AC�Ĵ�ֱƽ�����Ƿ�һ������Ϊ����˵�����ɣ�
����C��x2��y2�����F��1��0���ľ���ɵȲ����У��߶�AC�Ĵ�ֱƽ�����Ƿ�һ������Ϊ����˵�����ɣ�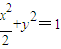 �������������빫ʽ���㵽ֱ�ߵľ��빫ʽ���ɼ���õ��ҽ���ľ����뵽ֱ��x=2�ľ���֮�ȵ�����Բ�������ʣ�
�������������빫ʽ���㵽ֱ�ߵľ��빫ʽ���ɼ���õ��ҽ���ľ����뵽ֱ��x=2�ľ���֮�ȵ�����Բ�������ʣ�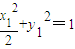 ��
�� ����ʽ���������ֱ��ACб�ʣ����߶�AC���е㣨m��n�����ɵ�бʽ�ɵ�AC��ֱƽ���߷��̣����е����깫ʽ�ɰѸô�ֱƽ���߷��̻�Ϊ֪������n�ķ��̣��ݴ˿ɵö��㣮
����ʽ���������ֱ��ACб�ʣ����߶�AC���е㣨m��n�����ɵ�бʽ�ɵ�AC��ֱƽ���߷��̣����е����깫ʽ�ɰѸô�ֱƽ���߷��̻�Ϊ֪������n�ķ��̣��ݴ˿ɵö��㣮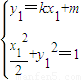 ��
��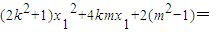 ����ֱ������Բ���еá�=0��x1=-
����ֱ������Բ���еá�=0��x1=- �٣���ֱ��PQ��ԲC2���У���
�٣���ֱ��PQ��ԲC2���У��� �ڣ������٢ڿ�����m���ɹ��ɶ����ɰ�|PQ|2��ʾΪr�ĺ��������û�������ʽ�ɵ������ֵ��
�ڣ������٢ڿ�����m���ɹ��ɶ����ɰ�|PQ|2��ʾΪr�ĺ��������û�������ʽ�ɵ������ֵ��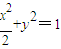 ��
��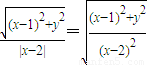 =
=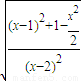 =
=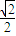 ��
��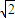 ��c=1������������e=
��c=1������������e=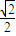 ��
��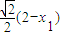 ��|BF|=
��|BF|=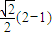 ��|CF|=
��|CF|=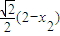 ��
��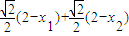 =2×
=2×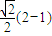 ������x1+x2=2��
������x1+x2=2��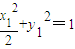 ��
��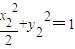 ����ʽ��������ã�
����ʽ��������ã�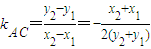 =-
=-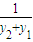 ��
��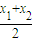 =1��n=
=1��n=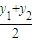 ��
�� ��0����
��0���� ��
��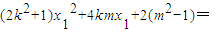 ��
��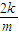 �٣�
�٣�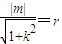 ����m2=r2��1+k2���ڣ�
����m2=r2��1+k2���ڣ�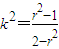 ����
����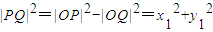 -r2=
-r2=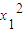 +��1-
+��1-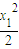 ��-r2
��-r2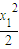 -r2=1+
-r2=1+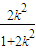 -r2=3-r2
-r2=3-r2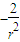
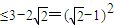 ����|PQ|��
����|PQ|�� -1��
-1��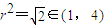 ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ�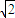 -1��
-1��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
| x2 |
| a2 |
| y2 |
| 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ������ϵxOy�У���Ǧ��Ͷ۽Ǧµ��ձ߷ֱ��뵥λԲ����A��B���㣮����A�ĺ�������
��ͼ����ƽ��ֱ������ϵxOy�У���Ǧ��Ͷ۽Ǧµ��ձ߷ֱ��뵥λԲ����A��B���㣮����A�ĺ�������| 3 |
| 5 |
| 12 |
| 13 |
| 16 |
| 65 |
| 16 |
| 65 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| m |
| y2 |
| 3 |
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 | t |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 16 |
| 7 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com