
���� ��1��ֱ��l�IJ���������ȥ������$\frac{y-2}{x-1}=\frac{{\frac{{\sqrt{2}}}{2}}}{m}=tan45��$���ɴ������m��ֵ���ɦ�2=x2+y2����cos��=x�����������M��ֱ�����귽�̣�
��2����$\left\{\begin{array}{l}x=1+\frac{{\sqrt{2}}}{2}t\\ y=2+\frac{{\sqrt{2}}}{2}t\end{array}\right.$����4x2-y2=4����$3{t^2}+4\sqrt{2}t-8=0$����t�ļ������������|PA|•|PB|��ֵ��
��� �⣺��1������б��Ϊ45���ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}x=1+mt\\ y=2+\frac{{\sqrt{2}}}{2}t\end{array}\right.$��tΪ��������
����ȥ������$\frac{y-2}{x-1}=\frac{{\frac{{\sqrt{2}}}{2}}}{m}=tan45��$�����$m=\frac{{\sqrt{2}}}{2}$������2�֣�
����M�ļ����귽��Ϊ��2��5cos2��-1��=4��
��5��2cos2��-��2=4��
�ߦ�2=x2+y2����cos��=x��
������M��ֱ�����귽��Ϊ4x2-y2=4������5�֣�
��2����$\left\{\begin{array}{l}x=1+\frac{{\sqrt{2}}}{2}t\\ y=2+\frac{{\sqrt{2}}}{2}t\end{array}\right.$����4x2-y2=4��
������$3{t^2}+4\sqrt{2}t-8=0$������8�֣�
��t�ļ��������$|{PA}|•|{PB}|=|{{t_1}•{t_2}}|=\frac{8}{3}$������10�֣�
���� ���⿼��ʵ��ֵ�����ߵ�ֱ�����귽�̵����������߶εij˻��������鼫���ꡢֱ������Ļ���������������֤�����������������������ת������˼�롢���ν��˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꽭��ʡ�ϲ��и�һ��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪�������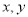 ��ֵ���±���ʾ�����
��ֵ���±���ʾ�����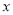 ��
��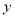 ������أ��һع�ֱ�߷���Ϊ
������أ��һع�ֱ�߷���Ϊ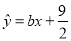 ����ʵ��
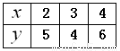
����ʵ��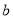 ��ֵΪ�� ��
��ֵΪ�� ��
A��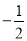 B��
B��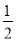 C��
C��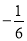 D��
D��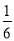
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꼪��ʡ��һ��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪A��B��C��������O�������ϣ�AB=BC=CA=3��������O��ƽ��ABC�ľ��������뾶�� ������O�ı����Ϊ �� ��
������O�ı����Ϊ �� ��
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢ڢ� | C�� | �ۢ� | D�� | �٢� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ��13+3$\sqrt{7}$��cm2 | B�� | ��12+4$\sqrt{3}$��cm2 | C�� | ��18+3$\sqrt{7}$��cm2 | D�� | $��9+3\sqrt{2}+3\sqrt{5}��c{m^2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 4+4�� | B�� | 4+3�� | C�� | 3+4�� | D�� | 3+3�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com