设f(x)是定义在[-1,1]上的奇函数,且其图象上任意两点连线的斜率均小于零.
(1)证明f(x)在[-1,1]上是减函数;
(2)如果f(x-c),f(x-c2)的定义域的交集为空集,求实数c的取值范围;
(3)证明:若-1≤c≤2,则f(x-c),f(x-c2)存在公共的定义域,并求出这个公共的定义域.
解:(1)由已知对任意的x
1、x
2∈[-1,1],且x
1≠x
2,
都有
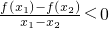
,从而x
1-x
2与f(x
1)-f(x
2)异号,
所以f(x)在[-1,1]上是减函数.
(2)因为f(x-c)的定义域是[c-1,c+1],f(x-c
2)的定义域是[c
2-1,c
2+1],
因为以上两个集合的交集为空集,所以c
2-1>c+1或c
2+1<c-1解得:c>2或c<-1
(3)因为c
2+1>c-1恒成立,有(2)问可知:当-1≤c≤2时,
f(x-c),f(x-c
2)存在公共的定义域.
若c
2-1≤c+1,即1≤c≤2或-1≤c≤0时,c
2+1≥c+1,c
2-1≥c-1,此时的交集是[c
2-1,c+1],即为公共的定义域;
若0<c<1,则c
2+1<c+1,c
2-1<c-1,此时的交集是[c-1,c
2+1],即为公共的定义域.
分析:(1)由已知对任意的x
1、x
2∈[-1,1],且x
1≠x
2,都有
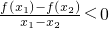
,从而x
1-x
2与f(x
1)-f(x
2)异号,所以f(x)在[-1,1]上是减函数.
(2)由f(x-c)的定义域得f(x-c
2)的定义域,根据题目条件可得关于c的不等式,通过求解可得c的取值范围.
(3)有(2)问可知:当-1≤c≤2时,f(x-c),f(x-c
2)存在公共的定义域.若c
2-1≤c+1,即1≤c≤2或-1≤c≤0时,c
2+1≥c+1,c
2-1≥c-1,此时的交集是[c
2-1,c+1];若0<c<1,则c
2+1<c+1,c
2-1<c-1,此时的交集是[c-1,c
2+1]
点评:本题考查了函数单调性的判断与证明,函数的定义域及其求法,注意对题目条件的灵活转化,是个中档题.

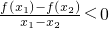 ,从而x1-x2与f(x1)-f(x2)异号,
,从而x1-x2与f(x1)-f(x2)异号,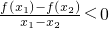 ,从而x1-x2与f(x1)-f(x2)异号,所以f(x)在[-1,1]上是减函数.
,从而x1-x2与f(x1)-f(x2)异号,所以f(x)在[-1,1]上是减函数.
