
【题目】如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
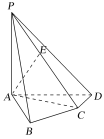
(1)求证:AE⊥平面PCD;
(2)求PB和平面PAD所成的角的大小;
(3)求二面角A-PD-C的正弦值.
【答案】(1)见证明;(2)45°(3)![]()
【解析】
(1)由线面垂直的性质可得![]() ,结合
,结合![]() ,可得
,可得![]() 平面
平面![]() ,由等腰三角形的性质可得
,由等腰三角形的性质可得![]() ,从而可得结果;(2) 先证明
,从而可得结果;(2) 先证明![]() 平面
平面![]() ,可得
,可得![]() 为
为![]() 和平面
和平面![]() 所成的角,判断
所成的角,判断![]() 是等腰直角三角形,从而可得结果;(3)过点
是等腰直角三角形,从而可得结果;(3)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,由(1)知,
,由(1)知,![]() 平面
平面![]() ,则
,则![]() 在平面
在平面![]() 内的射影是
内的射影是![]() ,则可证得
,则可证得![]() ,则
,则![]() 是二面角
是二面角![]() 的平面角,设
的平面角,设![]() ,可求得
,可求得![]()
![]() ,由直角三角形的性质可得结果.
,由直角三角形的性质可得结果.
(1)因为PA⊥底面ABCD
CD平面ABCD,故CD⊥PA.
因为CD⊥AC,PA∩AC=A,
所以CD⊥平面PAC.
又AE平面PAC,所以AE⊥CD.
由PA=AB=BC,∠ABC=60°,可得AC=PA.
因为E是PC的中点,所以AE⊥PC.
又PC∩CD=C,
所以AE⊥平面PCD.
(2)因为PA⊥底面ABCD,
AB平面ABCD,故PA⊥AB.
又AB⊥AD,PA∩AD=A,
所以AB⊥平面PAD,
故PB在平面PAD内的射影为PA,从而∠APB为PB和平面PAD所成的角.
在Rt△PAB中,AB=PA,
故∠APB=45°.
所以PB和平面PAD所成的角的大小为45°.
(3)过点E作EM⊥PD,垂足为M,连接AM,如图所示.
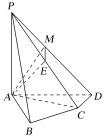
由(1)知,AE⊥平面PCD,则AM在平面PCD内的射影是EM,则可证得AM⊥PD.
因此∠AME是二面角A-PD-C的平面角.由已知可得∠CAD=30°.
设AC=a,
可得PA=a,AD=![]() a,PD=
a,PD=![]() a,AE=
a,AE=![]() a.
a.
在Rt△ADP中,
因为AM⊥PD,
所以AM·PD=PA·AD,
则AM=![]() =
=![]() a.
a.
在Rt△AEM中,
sin∠AME=![]() =
=![]() .
.
所以二面角A-PD-C的正弦值为![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
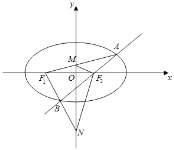
【题目】已知椭圆![]() ,
,![]() 为左、右焦点,直线
为左、右焦点,直线![]() 过
过![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点.
两点.
(1)若![]() 垂直于
垂直于![]() 轴时,求
轴时,求![]() ;
;
(2)当![]() 时,
时,![]() 在
在![]() 轴上方时,求
轴上方时,求![]() ,
,![]() 的坐标;
的坐标;
(3)若直线![]() 交
交![]() 轴于
轴于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,是否存在直线
,是否存在直线![]() ,使
,使![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在其图象上存在不同的两点
在其图象上存在不同的两点![]() ,
,![]() ,其坐标满足条件:
,其坐标满足条件: ![]() 的最大值为0,则称
的最大值为0,则称![]() 为“柯西函数”,则下列函数:①
为“柯西函数”,则下列函数:①![]()
![]() :②
:②![]() :③
:③![]() :④
:④![]() .
.
其中为“柯西函数”的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() .
.

(1)过![]() 作截面与线段
作截面与线段![]() 交于点
交于点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并予以证明;
的位置,并予以证明;
(2)在(1)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季取暖时减少能源消耗,业主决定对房屋的屋顶和外墙喷涂某种新型隔热材料,该材料有效使用年限为20年.已知房屋外表喷一层这种隔热材料的费用为每毫米厚6万元,且每年的能源消耗费用![]() (万元)与隔热层厚度
(万元)与隔热层厚度![]() (毫米)满足关系:
(毫米)满足关系:![]() .设
.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)请解释![]() 的实际意义,并求
的实际意义,并求![]() 的表达式;
的表达式;
(2)当隔热层喷涂厚度为多少毫米时,业主所付的总费用![]() 最少?并求此时与不建隔热层相比较,业主可节省多少钱?
最少?并求此时与不建隔热层相比较,业主可节省多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com