
分析 根据三角形三边关系判断得到A为最小角,C为直角,利用勾股定理列出关系式,与已知等式联立求出$\frac{a}{c}$的值,即为sinA的最小值.
解答 解:∵一个直角三角形的三边长a<b<c,
∴C为直角,A为最小角,
∴sinA的最小值为$\frac{a}{c}$,
∵$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}={c}^{2}}\\{{b}^{2}=ac}\end{array}\right.$,
∴a2+ac=c2,即$\frac{{a}^{2}}{{c}^{2}}$+$\frac{a}{c}$=1,
解得:$\frac{a}{c}$=$\frac{\sqrt{5}-1}{2}$.
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 此题考查了余弦定理,勾股定理,以及三角形三边关系,熟练掌握勾股定理是解本题的关键.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源:2016-2017学年河北涞水波峰中学高一9月月考数学试卷(解析版) 题型:选择题
已知非空集合M满足:若x∈M,则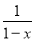 ∈M,则当4∈M时,集合M的所有元素之积等于( )
∈M,则当4∈M时,集合M的所有元素之积等于( )
A.0 B.1 C.-1 D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3π}{2}$,2π] | B. | ($\frac{3π}{2}$,2π) | C. | [$\frac{7π}{4}$,2π] | D. | ($\frac{7π}{4}$,2π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com