
分析 (1)连接PF1,则|PF1|=|PM|,由|PF1|+|PF2|=|MF2|=2$\sqrt{2}$>|F1F2|=2,利用椭圆的标准方程即可得出.
(2)当直线l斜率不存在时,不满足题意.当直线l斜率存在时,设N(x0,y0),设直线l:y-y0=k(x-x0),与椭圆方程$\frac{{x}^{2}}{2}+{y}^{2}$=1联立,利用直线与椭圆相切的性质可得:△=0,整理$({x}_{0}^{2}-2){k}^{2}$-2kx0y0+${y}_{0}^{2}$-1=0,又$\frac{{x}_{0}^{2}}{2}$+${y}_{0}^{2}$=1,解得k=-$\frac{{x}_{0}}{2{y}_{0}}$.直线l的方程与直线QF2的方程联立消去y即可得出.
解答 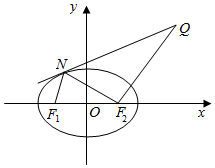 解:(1)连接PF1,则|PF1|=|PM|,∴|PF1|+|PF2|=|MF2|=2$\sqrt{2}$>|F1F2|=2,
解:(1)连接PF1,则|PF1|=|PM|,∴|PF1|+|PF2|=|MF2|=2$\sqrt{2}$>|F1F2|=2,
∴动点P的轨迹G是椭圆,设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
则2a=2$\sqrt{2}$,解得a=$\sqrt{2}$,又c=1,∴b2=a2-c2=1.
∴椭圆的标准方程为:$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(2)当直线l斜率不存在时,不满足题意.
当直线l斜率存在时,设N(x0,y0),则$\frac{{x}_{0}^{2}}{2}$+${y}_{0}^{2}$=1.
设直线l:y-y0=k(x-x0),与椭圆方程$\frac{{x}^{2}}{2}+{y}^{2}$=1联立化为:(1+2k2)x2+4k(y0-kx0)x+2$({y}_{0}-k{x}_{0})^{2}$-2=0,
△=16k2$({y}_{0}-k{x}_{0})^{2}$-4(1+2k2)[2$({y}_{0}-k{x}_{0})^{2}$-2]=0,整理$({x}_{0}^{2}-2){k}^{2}$-2kx0y0+${y}_{0}^{2}$-1=0,又$\frac{{x}_{0}^{2}}{2}$+${y}_{0}^{2}$=1,
∴${y}_{0}^{2}{k}^{2}$+kx0y0+$\frac{{x}_{0}^{2}}{4}$=0,∴$({y}_{0}k+\frac{{x}_{0}}{2})^{2}$=0,解得k=-$\frac{{x}_{0}}{2{y}_{0}}$.
∴直线l的方程化为:y=-$\frac{{x}_{0}}{2{y}_{0}}$(x-x0)+y0,①
直线QF2的方程为:$y=-\frac{{x}_{0}-1}{{y}_{0}}$(x-1),②.
①②联立消去y可得:$\frac{-\frac{{x}_{0}}{2{y}_{0}}(x-{x}_{0})+{y}_{0}}{x-1}$=$-\frac{{x}_{0}-1}{{y}_{0}}$,与${x}_{0}^{2}$+2${y}_{0}^{2}$=2联立可得:(x0-2)(x-2)=0.
∵$-\sqrt{2}≤{x}_{0}$$≤\sqrt{2}$,∴x0-2≠0,∴x=2.
∴交点Q的横坐标为2落在直线x=2上.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相切的性质、一元二次非常低根与系数的关系、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}}$](k∈Z) | B. | [kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}}$](k∈Z) | ||
| C. | [kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}}$](k∈Z) | D. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
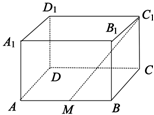 如图,长方体ABCD-A1B1C1D1中,AB=2,BC=$\sqrt{2}$,CC1=1,M为线段AB的中点.
如图,长方体ABCD-A1B1C1D1中,AB=2,BC=$\sqrt{2}$,CC1=1,M为线段AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥K) | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.635 | 10.828 |
| A. | 有99%以上的把握认为“爱好该项运动与性别有关” | |
| B. | 有99%以上的把握认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com