
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且其图象的一个对称轴为
,且其图象的一个对称轴为![]() ,将函数
,将函数![]() 图象上所有点的橫坐标缩小到原来的
图象上所有点的橫坐标缩小到原来的![]() 倍,再将图象向左平移
倍,再将图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象.
的图象.
(1)求![]() 的解析式,并写出其单调递增区间;
的解析式,并写出其单调递增区间;
(2)求函数![]() 在区间
在区间![]() 上的零点;
上的零点;
(3)对于任意的实数![]() ,记函数
,记函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
【答案】(1)![]() ,单调递增区间为
,单调递增区间为![]() ;
;
(2)![]() 、
、![]() 、
、![]() ;(3)
;(3)![]() .
.
【解析】
(1)由函数![]() 的最小正周期求出
的最小正周期求出![]() 的值,由图象的对称轴方程得出
的值,由图象的对称轴方程得出![]() 的值,从而可求出函数
的值,从而可求出函数![]() 的解析式;
的解析式;
(2)先利用图象变换的规律得出函数![]() 的解析式,然后在区间
的解析式,然后在区间![]() 上解方程
上解方程![]() 可得出函数
可得出函数![]() 的零点;
的零点;
(3)对![]() 分三种情况
分三种情况![]() 、
、![]() 、
、![]() 分类讨论,分析函数
分类讨论,分析函数![]() 在区间
在区间![]() 上的单调性,得出
上的单调性,得出![]() 和
和![]() ,可得出
,可得出![]() 关于
关于![]() 的表达式,再利用函数
的表达式,再利用函数![]() 的单调性得出函数
的单调性得出函数![]() 的最大值.
的最大值.
(1)由题意可知,![]() ,
,![]() .
.
令![]() ,即
,即![]() ,
,
即函数![]() 的图象的对称轴方程为
的图象的对称轴方程为![]() .
.
由于函数![]() 图象的一条对称轴方程为
图象的一条对称轴方程为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,则
,则![]() ,因此,
,因此,![]() .
.
函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
(2)将函数![]() 的图象上所有点的橫坐标缩小到原来的
的图象上所有点的橫坐标缩小到原来的![]() 倍,得到函数
倍,得到函数![]() .
.
再将所得函数的图象向左平移![]() 个单位长度,
个单位长度,
得到函数![]() .
.
令![]() ,即
,即![]() ,化简得
,化简得![]() ,
,
得![]() 或
或![]() .
.
由于![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 或
或![]() .
.
因此,函数![]() 在
在![]() 上的零点为
上的零点为![]() 、
、![]() 、
、![]() ;
;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以,![]() ,由于
,由于![]() ,
,![]() ,
,
此时,![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以,![]() ,由于
,由于![]() ,
,![]() ,
,
此时,![]() ;
;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以,![]() ,
,![]() ,
,
此时,![]() .
.
所以,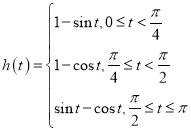 .
.
当![]() 时,函数
时,函数![]() 单调递减,
单调递减,![]() ;
;
当![]() 时,函数
时,函数![]() 单调递增,此时
单调递增,此时![]() ;
;
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
综上所述:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
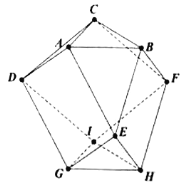
【题目】在如图所示的十一面体![]() 中,用
中,用![]() 种不同颜色给这个几何体各个顶点染色,每个顶点染一种颜色,要求每条棱的两端点异色,则不同的染色方案种数为__________.
种不同颜色给这个几何体各个顶点染色,每个顶点染一种颜色,要求每条棱的两端点异色,则不同的染色方案种数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() (万元)与销售
(万元)与销售![]() (万元)之间有如下的对应数据:
(万元)之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
若由资料可知![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)据此估计广告费用支出为10万元时销售收入![]() 的值.
的值.
(参考公式:
 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于 x 的函数f(x)=lg(x2﹣2x﹣3)的定义域为集合 A,函数 g(x)=x﹣a,(0≤x≤4)的值域为集合 B.
(1)求集合 A,B;
(2)若集合 A,B 满足 A∩B=B,求实数 a 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C所对的边为a、b、c,且 ![]() asinC﹣c(2+cosA)=0.
asinC﹣c(2+cosA)=0.
(1)求角A的大小;
(2)若△ABC的最大边长为 ![]() ,且sinC=2sinB,求最小边长.
,且sinC=2sinB,求最小边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M(x,y)到直线l:x=3的距离是它到点D(1,0)的距离的 ![]() 倍.
倍.
(1)求动点M的轨迹C的方程;
(2)设轨迹C上一动点T满足: ![]() =2λ
=2λ ![]() +3μ
+3μ ![]() ,其中P、Q是轨迹C上的点,且直线OP与OQ的斜率之积为﹣
,其中P、Q是轨迹C上的点,且直线OP与OQ的斜率之积为﹣ ![]() .若N(λ,μ)为一动点,F1(﹣
.若N(λ,μ)为一动点,F1(﹣ ![]() ,0)、F2(
,0)、F2( ![]() ,0)为两定点,求|NF1|+|NF2|的值.
,0)为两定点,求|NF1|+|NF2|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(Ⅰ)求ω的值和f(x)的单调递增区间;
(Ⅱ)若关于x的方程f(x)﹣m=0在区间[0,![]() ]上有两个实数解,求实数m的取值范围.
]上有两个实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子的繁殖问题时,发现有这样的一列数:1,1,2,3,5,8,…,该数列的特点是:前两个数均为1,从第三个数起,每一个数都等于它前面两个数的和.人们把这样的一列数组成的数列{an}称为斐波那契数列,则 ![]() ﹣
﹣ ![]() =( )
=( )
A.0
B.﹣1
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() 且
且![]() ,在数列
,在数列![]() 中,首项
中,首项![]() ,
,![]() 是其前
是其前![]() 项和,且
项和,且![]() ,
,![]() .
.
(1)设![]() ,
,![]() ,证明数列
,证明数列![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() ,证明数列
,证明数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(3)若当且仅当![]() 时,数列
时,数列![]() 取到最小值,求
取到最小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com