
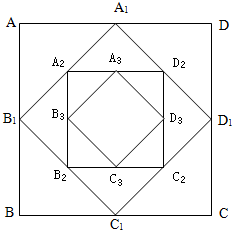
 如图,在面积为4的正方形ABCD中,连接各边中点得正方形A1B1C1D1,此时正方形A1B1C1D1的面积记作a1;再连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,此时正方形A2B2C2D2的面积记作a2;…;如此继续下去,得到一个数列{an}.
如图,在面积为4的正方形ABCD中,连接各边中点得正方形A1B1C1D1,此时正方形A1B1C1D1的面积记作a1;再连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,此时正方形A2B2C2D2的面积记作a2;…;如此继续下去,得到一个数列{an}.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(
| ||||
1-
|
| 1 |
| 2 |


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
 如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个圆的面积之和,则
如图,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设Sn为前n个圆的面积之和,则| lim |
| n→∞ |
| A、2πr2 | ||
B、
| ||
| C、4πr2 | ||
| D、6πr2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年新人教版高三上学期单元测试(5)数学试卷 题型:选择题
如图,在半径为r 的圆内作内接正六边形,再作正六边形的内切圆,又在此内切
圆内作内接正六边形,如此无限继续下去,设 为前n个圆的面积之和,则
为前n个圆的面积之和,则
 =( )
=( )

A.2 B.
B.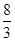

C.4 D.6
D.6
查看答案和解析>>
科目:高中数学 来源:2010年高考数学试卷精编:12.2 极限与连续性(解析版) 题型:选择题
 sn=( )
sn=( )
 πr2
πr2查看答案和解析>>
科目:高中数学 来源:2010年湖北省高考数学试卷(理科)(解析版) 题型:选择题
 sn=( )
sn=( )
 πr2
πr2查看答案和解析>>
科目:高中数学 来源:湖北省高考真题 题型:单选题


 πr2
πr2 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com