
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
| 甲 | | 乙 |
| 6 | 9 | 3 6 7 9 9 |
| 9 5 1 0 | 8 | 0 1 5 6 |
| 9 9 4 4 2 | 7 | 3 4 5 8 8 8 |
| 8 8 5 1 1 0 | 6 | 0 7 7 |
| 4 3 3 2 | 5 | 2 5 |
| | 甲班(A方式) | 乙班(B方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)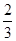 (2)详见解析
(2)详见解析
解析试题分析:(1)本题是一个等可能事件的概率,试验发生包含的事件是从不低于86分的成绩中随机抽取两个包含的基本事件数,列举出结果,满足条件的事件也可以列举出结果,得到概率.
(2)根据所给的数据,列出列联表,根据列联表中的数据,做出观测值,把观测值同临界值表进行比较,得到有90%的把握认为成绩优秀与教学方式有关.
试题解析:解析 (1)设“抽出的两个均‘成绩优秀’”为事件A.
从不低于86分的成绩中随机抽取2个的基本事件为(86,93),(86,96),(86,97),(86,99),(86,99),(93,96),(93,97),(93,99),(93,99),(96,97),(96,99),(96,99),(97,99),(97,99),(99,99),共15个.
而事件A包含基本事件:
(93,96),(93,97),(93,99),(93,99),(96,97),(96,99),(96,99),(97,99),(97,99),(99,99),共10个.
所以所求概率为P(A)= =
=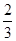 .
.
(2)由已知数据得 甲班(A方式) 乙班(B方式) 总计 成绩优秀 1 5 6 成绩不优秀 19 15 34 总计 20 20 40
根据列联表中数据,
K2= ,
,
由于3.137>2.706,所以有90%的把握认为“成绩优秀”与教学方式有关.
考点:1.茎叶图;2.独立性检验.


科目:高中数学 来源: 题型:解答题
为了解某班关注NBA(美国职业篮球)是否与性别有关,对某班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
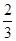 .
.| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
商场销售的某种饮品每件售价为36元,成本为20元.对该饮品进行促销:顾客每购买一件,当即连续转动三次如图所示转盘,每次停止后指针向一个数字,若三次指向同一个数字,获一等奖;若三次指向的数字是连号(不考虑顺序),获二等奖;其他情况无奖.
(1)求一顾客一次购买两件该饮品,至少有一件获得奖励的概率;
(2)若奖励为返还现金,一等奖奖金数是二等奖的2倍,统计表明:每天的销售y(件)与一等奖的奖金额x(元)的关系式为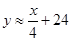 ,问x设定为多少最佳?并说明理由.
,问x设定为多少最佳?并说明理由.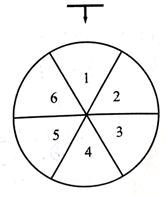
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·洛阳模拟)现有一批产品共有10件,其中8件为正品,2件为次品.
(1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率.
(2)如果从中一次取3件,求3件都是正品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
黄山旅游公司为了体现尊师重教,在每年暑假期间对来黄山旅游的全国各地教师和学生,凭教师证和学生证实行购买门票优惠.某旅游公司组织有22名游客的旅游团到黄山旅游,其中有14名教师和8名学生.但是只有10名教师带了教师证,6名学生带了学生证.
(1)在该旅游团中随机采访3名游客,求恰有1人持有教师证且持有学生证者最多1人的概率;
(2)在该团中随机采访3名学生,设其中持有学生证的人数为随机变量ξ,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以0为起点,再从 ,
, (如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。
(如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。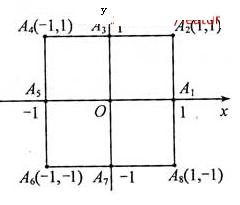
(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙两人进行乒乓球比赛,各局相互独立,约定每局胜者得1分,负者得0分,如果两人比赛五局,乙得1分与得2分的概率恰好相等.
求乙在每局中获胜的概率为多少?
假设比赛进行到有一人比对方多2分或打满6局时停止,用 表示比赛停止时已打局数,求
表示比赛停止时已打局数,求 的期望
的期望 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com