
【题目】(导学号:05856309)
已知抛物线C的方程为x2=4y,M(2,1)为抛物线C上一点,F为抛物线的焦点.
(Ⅰ)求|MF|;
(Ⅱ)设直线l2:y=kx+m与抛物线C有唯一公共点P,且与直线l1:y=-1相交于点Q,试问,在坐标平面内是否存在点N,使得以PQ为直径的圆恒过点N?若存在,求出点N的坐标,若不存在,说明理由.
【答案】(1)2;(2) 在坐标平面内存在点N,使得以PQ为直径的圆恒过点N,其坐标为(0,1)
【解析】试题分析:(1)求得抛物线的焦点和准线方程,根据抛物线的定义,即可得到所求|MF|;
(2)假设存在点N,使得以PQ为直径的圆恒过点N,由直线l2:y=kx+m与抛物线C有唯一公共点P知,直线l2与抛物线C相切,利用导数求出直线l2的方程,进而求出Q点坐标,根据直径所对的圆周角为直角,利用![]() ,求出N点坐标.
,求出N点坐标.
试题解析:
(Ⅰ)由题可知2p=4,即p=2,由抛物线的定义可知|MF|=1+![]() =2.
=2.
(Ⅱ)由C关于y轴对称可知,若存在点N,使得以PQ为直径的圆恒过点N,则点N必在y轴上.
设N(0,n),又设点P(x0,![]() ),由直线l2:y=kx+m与曲线C有唯一公共点P知,直线l2与C相切.
),由直线l2:y=kx+m与曲线C有唯一公共点P知,直线l2与C相切.
由y=x2得y′=x,∴![]() ,
,
∴直线l2的方程为y-![]() =
=![]() (x-x0),
(x-x0),
令y=-1得x=![]() ,
,
∴Q点的坐标为(![]() -
-![]() ,-1),
,-1),
∴![]() =(x0,
=(x0,![]() -n),
-n),![]() =(
=(![]() -
-![]() ,-1-n).
,-1-n).
∵点N在以PQ为直径的圆上,
∴![]() ·
·![]() =
=![]() -2-(1+n)(
-2-(1+n)(![]() -n)
-n)
=(1-n)![]() +n2+n-2=0,①
+n2+n-2=0,①
要使方程①对x0恒成立,
必须有![]() 解得n=1,
解得n=1,
∴在坐标平面内存在点N,使得以PQ为直径的圆恒过点N,其坐标为(0,1).


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
【题目】(导学号:05856264)
已知函数f(x)=aln x,e为自然对数的底数.
(Ⅰ)曲线f(x)在点A(1,f(1))处的切线与坐标轴所围成的三角形的面积为2,求实数a的值;
(Ⅱ)若f(x)≥1-![]() 恒成立,求实数a的值取值范围.
恒成立,求实数a的值取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“扶贫帮困”是中华民族的传统美德,某校为帮扶困难同学,采用如下方式进行一次募捐:在不透明的箱子中放入大小均相同的白球七个,红球三个,每位献爱心的参与者投币20元有一次摸奖机会,一次性从箱子中摸球三个(摸完球后将球放回),若有一个红球,奖金10元,两个红球奖金20元,三个全是红球奖金100元.
(1)求献爱心参与者中将的概率;
(2)若该次募捐900位献爱心参与者,求此次募捐所得善款的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)一位网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的![]() 五种商品有购买意向.已知该网民购买
五种商品有购买意向.已知该网民购买![]() 两种商品的概率均为
两种商品的概率均为![]() ,购买
,购买![]() 两种商品的概率均为
两种商品的概率均为![]() ,购买
,购买![]() 种商品的概率为
种商品的概率为![]() .假设该网民是否购买这五种商品相互独立.
.假设该网民是否购买这五种商品相互独立.
(1)求该网民至少购买4种商品的概率;
(2)用随机变量![]() 表示该网民购买商品的种数,求
表示该网民购买商品的种数,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856299)已知双曲线![]() (a>0,b>0)的左、右焦点分别是F1,F2,点P是其上一点,双曲线的离心率是2,若△F1PF2是直角三角形且面积为3,则双曲线的实轴长为( )
(a>0,b>0)的左、右焦点分别是F1,F2,点P是其上一点,双曲线的离心率是2,若△F1PF2是直角三角形且面积为3,则双曲线的实轴长为( )
A. 2 B. ![]() C. 2或
C. 2或![]() D. 1或
D. 1或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届吉林省普通中学高三第二次调研】某校冬令营有三名男同学A,B,C和三名女同学X,Y,Z,
(1)从6人中抽取2人参加知识竞赛,求抽取的2人都是男生的概率;
(2)若从这3名男生和3名女生中各任选一名,求这2人中包含A且不包含X的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856332)
已知三棱柱ABC-A1B1C1如图所示,其中CA⊥平面ABB1A1,四边形ABB1A1为菱形,∠AA1B1=60°,E为BB1的中点,F为CB1的中点.
(Ⅰ)证明:平面AEF⊥平面CAA1C1;
(Ⅱ)若CA=2,AA1=4,求B1到平面AEF的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:f(x)=![]() 在区间(1,+∞)上是减函数;q:若x1,x2是方程x2-ax-2=0的两个实根,则不等式m2+5m-3≥|x1-x2|对任意实数a∈[-1,1]恒成立.若p不正确,q正确,求实数m的取值范围.
在区间(1,+∞)上是减函数;q:若x1,x2是方程x2-ax-2=0的两个实根,则不等式m2+5m-3≥|x1-x2|对任意实数a∈[-1,1]恒成立.若p不正确,q正确,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在标准温度和大气压下,人体血液中氢离子的物质的量的浓度(单位mol/L,记作![]() )和氢氧根离子的物质的量的浓度(单位mol/L,记作
)和氢氧根离子的物质的量的浓度(单位mol/L,记作![]() )的乘积等于常数
)的乘积等于常数![]() .已知pH值的定义为
.已知pH值的定义为![]() ,健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的
,健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的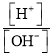 可以为(参考数据:
可以为(参考数据: ![]() ,
, ![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com