
【题目】已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,0<φ<π),其导函数f′(x)的部分图象如图所示,则函数f(x)的解析式为( ) 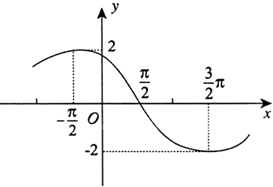
A.f(x)=4sin( ![]() x+
x+ ![]() π)
π)
B.f(x)=4sin( ![]() x+
x+ ![]() )
)
C.f(x)=4sin( ![]() x+
x+ ![]() )
)
D.f(x)=4sin( ![]() x+
x+ ![]() )
)
科目:高中数学 来源: 题型:
【题目】定义在D上的函数 ![]() ,若满足:
,若满足: ![]() ,都有
,都有 ![]() 成立,则称
成立,则称 ![]() 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数 ![]() 的上界.
的上界.
(I)设 ![]() ,证明:
,证明: ![]() 在
在 ![]() 上是有界函数,并写出
上是有界函数,并写出 ![]() 所有上界的值的集合;
所有上界的值的集合;
(II)若函数 ![]() 在
在 ![]() 上是以3为上界的有界函数,求实数a的取值范围.
上是以3为上界的有界函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
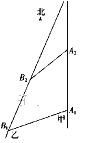
【题目】如图,甲船以每小时30![]() 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)如图所示的茎叶图记录了甲、乙两组各四名同学的投篮命中次数, 乙组记录中有一个数据模糊,无法确认, 在图中以![]() 表示.
表示.
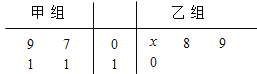
(Ⅰ)如果乙组同学投篮命中次数的平均数为![]() , 求
, 求![]() 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(Ⅱ)在(Ⅰ)的条件下, 分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名, 记事件A:“两名同学的投篮命中次数之和为17”, 求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
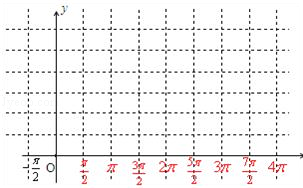
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出f(x)的周期、振幅、初相、对称轴;
(3)此函数图象由y=sinx的图象怎样变换得到?(注:y轴上每一竖格长为1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知抛物线 C1:y2=2px (p>0),直线 l 与抛物线 C 相交于 A、B 两点,且当倾斜角为 60°的直线 l 经过抛物线 C1 的焦点 F 时,有|AB|= ![]() .
.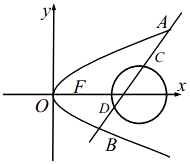
(Ⅰ)求抛物线 C 的方程;
(Ⅱ)已知圆 C2:(x﹣1)2+y2= ![]() ,是否存在倾斜角不为 90°的直线 l,使得线段 AB 被圆 C2 截成三等分?若存在,求出直线 l 的方程;若不存在,请说明理由.
,是否存在倾斜角不为 90°的直线 l,使得线段 AB 被圆 C2 截成三等分?若存在,求出直线 l 的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式|x﹣a|<b的解集为{x|2<x<4}.
(Ⅰ)求实数a,b的值;
(Ⅱ)设实数x,y,z 满足 ![]() +
+ ![]() +
+ ![]() =1,求x,y,z的最大值和最小值.
=1,求x,y,z的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a1+a2=10,a5=a3+4.
(1)求{an}的通项公式;
(2)记{an}的前n项和为Sn若Sk+1<2ak+a2,求正整数k的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com