
����Ŀ��ij����Ӷ������˶�Ա�������ܽ���ͳ���о�����������˶�Ա��Ͷ������ʱ���˶�Ա���������ĵ�ˮƽ��������ָ�꣬��ij�˶�Ա���������ɳ��ε�ͳ�ƣ�����ͳ�ƽ����������Ƶ�ʷֲ�ֱ��ͼ��
��������Ƶ�ʷֲ�ֱ��ͼ������˶�ԱͶ������ʱ�������������ĵ�ˮƽ�������λ����
������ij�������У�������ǰ4��Ͷ�����е��������ĵ�ˮƽ�������������ҹ涨���˶�ԱͶ������ʱ�������������ĵ�ˮƽ���벻����4�ļ�1�֣�����۵�1�֣����������X��ʾ��4��Ͷ������ܷ֣���Ƶ����Ϊ���ʣ���X�ķֲ��к���ѧ������
���𰸡��⣺��I�� ����˶�Ա�������ˮƽ�������λ��Ϊx��
��0.05��2+0.10+0.20��0.5���ң�0.40+0.20����1=0.6��0.5��
��x��[4��5]
��0.40����5��x��+0.20��1=0.5�����x=4.25��
����˶�Ա�������ˮƽ�������λ����4.25���ף���
������Ƶ�ʷֲ�ֱ��ͼ��Ͷ������ʱ����������볬��4�ĸ���Ϊp= ![]() ��
��
��������ε����п���ȡֵΪ��4����2��0��2��4��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��X�ķֲ���Ϊ��
X | ��4 | ��2 | 0 | 2 | 4 |
P |
|
|
|
|
|
EX=����4���� ![]() +����2����
+����2���� ![]() +0��
+0�� ![]() +2��
+2�� ![]() +4��
+4�� ![]() =
= ![]()
����������I�� ����˶�Ա�������ˮƽ�������λ��Ϊx���Ƶ���0.40����5��x��+0.20��1=0.5���ɴ���������˶�Ա�������ˮƽ�������λ����������Ƶ�ʷֲ�ֱ��ͼ��Ͷ������ʱ����������볬��4�ĸ���Ϊp= ![]() ����������ε����п���ȡֵΪ��4����2��0��2��4���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��
����������ε����п���ȡֵΪ��4����2��0��2��4���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��
�����㾫����������Ĺؼ�����������ɢ�������������ֲ��е����֪ʶ���������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �IJ���ͼ����ͼ��ʾ.
�IJ���ͼ����ͼ��ʾ.

��1������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����ͼ��![]() ��ֵ������
��ֵ������![]() �ĵ����ݼ����䣻
�ĵ����ݼ����䣻
��3������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ�õ�
����λ�õ�![]() ��ͼ�����ֱ��
��ͼ�����ֱ��![]() �Գƣ���
�Գƣ���![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��CΪ��O�����㣬BΪ ![]() ���е㣬PΪAC�ӳ�����һ�㣬PQ���O�����ڵ�Q��BQ��AC�ཻ�ڵ�D��
���е㣬PΪAC�ӳ�����һ�㣬PQ���O�����ڵ�Q��BQ��AC�ཻ�ڵ�D��
����֤������DPQΪ���������Σ�
������PC=1��AD=PD����BDQD��ֵ��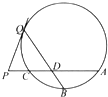
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��=x3+ax2+bx��a��b��R����ͼ����x��������һ��A��m��0����m��0������f��x���ļ���ֵΪ ![]() ����m��ֵΪ�� ��
����m��ֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l�IJ�������Ϊ (tΪ����)����C�IJ�������Ϊ
(tΪ����)����C�IJ�������Ϊ![]() ��
��![]() ����
Ϊ����![]() ��������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ����P�ļ�����Ϊ
��������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ����P�ļ�����Ϊ![]()
��![]() ������ֱ��l�Լ�����C�ļ����귽�̣�
������ֱ��l�Լ�����C�ļ����귽�̣�
��������ֱ��l������C����A��B���㣬��������PAB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=ex��ax2��2x+b��eΪ��Ȼ�����ĵ�����a��b��R����
������f�䣨x��Ϊf��x���ĵ�������֤������a��0ʱ��f�䣨x������СֵС��0��
������a��0��f��x����0������������������������b��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �ҷֱ���������������ֱ�ߵ�һ��ʽ����.
�ҷֱ���������������ֱ�ߵ�һ��ʽ����.
��1����б��Ϊ45�㣻
��2����![]() ���ϵĽؾ�Ϊ5��
���ϵĽؾ�Ϊ5��
��3���ڵڶ�������������Χ�ɵ����������Ϊ4.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��
��![]() �ϵĵ�
�ϵĵ�![]() ���佹��
���佹��![]() �ľ���Ϊ
�ľ���Ϊ![]() .
.
������![]() �ķ��̣�
�ķ��̣�
���� ��ֱ֪��![]() ������
������![]() ����
����![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬��ֱ��
���㣬��ֱ��![]() ��ֱ��
��ֱ��![]() ��б��֮��Ϊ1��֤����
��б��֮��Ϊ1��֤����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ����������
����������![]() ��
��![]() ��
��
��1������![]() ����С�������뵥���ݼ����䣻
����С�������뵥���ݼ����䣻
��2����![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��ǽ�
�ֱ��ǽ�![]() ��
��![]() ��
��![]() �ĶԱߣ���֪
�ĶԱߣ���֪![]() ��
��![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ���Բ�뾶
���Բ�뾶![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com