
【题目】设函数f(x)=ex(sinx﹣cosx)(0≤x≤2016π),则函数f(x)的各极大值之和为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解::∵函数f(x)=ex(sinx﹣cosx),
∴f′(x)=[ex(sinx﹣cosx)]′=ex(sinx﹣cosx)+ex(cosx+sinx)=2exsinx;
令f′(x)=0,解得x=kπ(k∈Z);
∴当2kπ<x<2kπ+π时,f′(x)>0,原函数单调递增,
当2kπ+π<x<2kπ+2π时,f′(x)<0,原函数单调递减;
∴当x=2kπ+π时,函数f(x)取得极大值,
此时f(2kπ+π)=e2kπ+π[sin(2kπ+π)﹣cos(2kπ+π)]=e2kπ+π;
又∵0≤x≤2016π,∴0和2016π都不是极值点,
∴函数f(x)的各极大值之和为:
eπ+e3π+e5π+…+e2015π= ![]() ,
,
所以答案是:D.
【考点精析】认真审题,首先需要了解函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值).
是极小值).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={1,3,5,7},B={x|(2x﹣1)(x﹣5)>0},则A∩(RB)( )
A.{1,3}
B.{1,3,5}
C.{3,5}
D.{3,5,7}
查看答案和解析>>
科目:高中数学 来源: 题型:
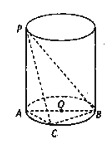
【题目】如图所示, ![]() 是圆柱的母线,
是圆柱的母线, ![]() 是圆柱底面圆的直径,
是圆柱底面圆的直径, ![]() 是底面圆周上异于
是底面圆周上异于![]() 的任意一点,
的任意一点, ![]() .
.
(1)求证: ![]() ;
;
(2)求三棱锥![]() 体积的最大值,并写出此时三棱锥
体积的最大值,并写出此时三棱锥![]() 外接球的表面积.
外接球的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线过点P(﹣3 ![]() ,4),它的渐近线方程为y=±
,4),它的渐近线方程为y=± ![]() x.
x.
(1)求双曲线的标准方程;
(2)设F1和F2为该双曲线的左、右焦点,点P在此双曲线上,且|PF1||PF2|=41,求∠F1PF2的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com