
【题目】梯形![]() 顶点
顶点![]() 在以
在以![]() 为直径的圆上,
为直径的圆上,![]() 米.
米.
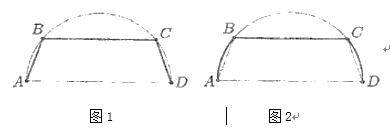
(1)如图1,若电热丝由![]() 这三部分组成,在
这三部分组成,在![]() 上每米可辐射1单位热量,在
上每米可辐射1单位热量,在![]() 上每米可辐射2单位热量,请设计
上每米可辐射2单位热量,请设计![]() 的长度,使得电热丝的总热量最大,并求总热量的最大值;
的长度,使得电热丝的总热量最大,并求总热量的最大值;
(2)如图2,若电热丝由弧![]() 和弦
和弦![]() 这三部分组成,在弧
这三部分组成,在弧![]() 上每米可辐射1单位热量,在弦
上每米可辐射1单位热量,在弦![]() 上每米可辐射2单位热量,请设计
上每米可辐射2单位热量,请设计![]() 的长度,使得电热丝辐射的总热量最大.
的长度,使得电热丝辐射的总热量最大.
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an=logn+1(n+2)(n∈N*)定义使a1a2…ak为整数的数k叫做企盼数,则区间[1,2019]内所有的企盼数的和是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考虑某长方体的三个两两相邻的面上的三条对角线及体对角线(共四条线段),则正确的命题是( )
A. 必有某三条线段不能组成一个三角形的三边
B. 任何三条线段都可组成三角形,其每个内角都是锐角
C. 任何三条线段都可组成三角形,其中必有一个是钝角三角形
D. 任何三条线段都可组成三角形,其形状是“锐角的”或是“非锐角的”,随长方体的长、宽、高而变化,不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明理由.
附:![]()
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,从外表上看,六根等长的正四棱柱分成三组,经![]() 榫卯起来,如图,若正四棱柱的高为
榫卯起来,如图,若正四棱柱的高为![]() ,底面正方形的边长为
,底面正方形的边长为![]() ,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为( )(容器壁的厚度忽略不计)
,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为( )(容器壁的厚度忽略不计)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com