练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    定义一种运算法则：
    .
    ab
    cd
    .
    =ad-bc    ，若
    .
    sin
    θ
    2
    -cos
    θ
    2
    cos
    3θ
    2
    sin
    3θ
    2
    .
    =
    		3
    2
    ，则cosθ=
    		3
    2
    		3
    2
    ．
    分析：利用
    .
    ab
    cd
    .
    =ad-bc    ，将原等式等价转化为三角函数等式，可解．
    解答：解：由题意，
    .
    sin
    θ
    2
    -cos
    θ
    2
    cos
    3θ
    2
    sin
    3θ
    2
    .
    =sin
    θ
    2
    sin
    3θ
    2
    +cos
    θ
    2
    cos
    3θ
    2
    =cosθ=
    		3
    2
    ，
    故答案为
    		3
    2
    ．
    点评：本题主要考查二阶行列式的定义，考查三角函数的和角公式，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：黄冈中学　高二数学(下册)、考试卷5　简单几何体同步测试卷(二) 题型：044

    如图，已知向量，可构成空间向量的一组基底，若，在向量已有的运算法则基础上，新定义一种运算．显然的结果仍为一向量．

    (1)求证：向量p为平面OAB的法向量；

    (2)求证：以OA，OB为边的平行四边形OADB的面积等于；

    (3)得到四边形OADB按向量平移，得到一个平行六面体，试判断平行六面体的体积V与的大小关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知向量，可构成空间向量的一个基底，若

    ，在向量已有的运算法则的基础上，新定义一种运算，显然的结果仍为一向量，记作．

    求证：向量为平面的法向量；

    求证：以为边的平行四边形的面积等于；

    将四边形按向量平移，得到一个平行六面体，试判断平行六面体的体积与的大小．

    查看答案和解析>>

    科目：高中数学 来源：2013届江西省高二上学期第二次月考理科数学试卷 题型：解答题

    如图，已知向量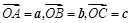，可构成空间向量的一个基底，若，在向量已有的运算法则的基础上，新定义一种运算，显然的结果仍为一向量，记作．

    1、求证：向量为平面的法向量；

    2、求证：以为边的平行四边形的面积等于；

    将四边形按向量平移，得到一个平行六面体，试判断平行六面体的体积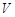与的大小．

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年江苏省南京一中高一（上）期末数学试卷（解析版） 题型：填空题

    定义一种运算法则：，若，则cosθ=    ．

    查看答案和解析>>

    同步练习册答案