
【题目】若![]() 是素数,证明存在0,1,2,…,
是素数,证明存在0,1,2,…,![]() 的一个排列(
的一个排列(![]() ,
,![]() ,…,
,…,![]() ),使得
),使得![]() ,
,![]() ,
,![]() ,…,
,…,![]() .被
.被![]() 除的余数各不相同.
除的余数各不相同.
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】我国有一道古典数学名著——两鼠穿墙:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”题意是:“有两只老鼠从墙的两边打洞穿墙(连线与墙面垂直),大老鼠第一天进一尺,以后每天加倍,小老鼠第一天也进一尺,以后每天减半,那么两鼠第几天能见面.”假设墙厚16尺,如图是源于该题思想的一个程序框图,则输出的![]() ( )
( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=![]() x+4,动圆⊙O:x2+y2=r2(1<r<2),菱形ABCD的一个内角为60°,顶点A、B在直线l上,顶点C、D在⊙O上.当r变化时,求菱形ABCD的面积S的取值范围.
x+4,动圆⊙O:x2+y2=r2(1<r<2),菱形ABCD的一个内角为60°,顶点A、B在直线l上,顶点C、D在⊙O上.当r变化时,求菱形ABCD的面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在时钟的表盘上作9个![]() 的扇形,每一个都覆盖4个数字,每两个覆盖的数字不全相同.求证:一定可以找到3个扇形,恰好覆盖整个表盘.举一个反例说明,作8个扇形将不具有上述性质.
的扇形,每一个都覆盖4个数字,每两个覆盖的数字不全相同.求证:一定可以找到3个扇形,恰好覆盖整个表盘.举一个反例说明,作8个扇形将不具有上述性质.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某辆汽车以![]() 千米
千米![]() 小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求
小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求![]() 时,每小时的油耗(所需要的汽油量)为
时,每小时的油耗(所需要的汽油量)为![]() 升,其中
升,其中![]() 为常数,且
为常数,且![]() .
.
(1)若汽车以120千米![]() 小时的速度行驶时,每小时的油耗为11.5升,欲使每小时的油耗不超过9升,求
小时的速度行驶时,每小时的油耗为11.5升,欲使每小时的油耗不超过9升,求![]() 的取值范围;
的取值范围;
(2)求该汽车行驶100千米的油耗的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线y=ax+1和抛物线y2=4x相交于不同的A,B两点.
(Ⅰ)若a=-2,求弦长|AB|;
(Ⅱ)若以AB为直径的圆经过原点O,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() ,
,![]() ,…,
,…,![]() 是一个数列,对每个
是一个数列,对每个![]() ,
,![]() ,
,![]() .如果
.如果![]() ,
,![]() 两数不同,写
两数不同,写![]() ;如果
;如果![]() ,
,![]() 两数相同,写
两数相同,写![]() .于是得到一个新数列
.于是得到一个新数列![]() ,
,![]() ,…,
,…,![]() ,其中
,其中![]() .重复上述方法,得到一个由0及1两个数字组成的三角形数表,最后一行仅一个数字,求这张数字表中1的和的最大值.
.重复上述方法,得到一个由0及1两个数字组成的三角形数表,最后一行仅一个数字,求这张数字表中1的和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题统计结果如图表所示.
人,回答问题统计结果如图表所示.
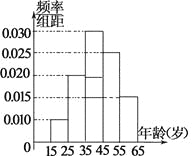
组号 | 分组 | 回答正确 | 回答正确的人数 |
第1组 |
| 5 | 0.5 |
第2组 |
|
| 0.9 |
第3组 |
| 27 |
|
第4组 |
|
| 0.36 |
第5组 |
| 3 |
|
(Ⅰ) 分别求出![]() 的值;
的值;
(Ⅱ) 从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(Ⅲ) 在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com