取空间中有三条侧棱两两垂直的四面体A-BCD,且AB=a,AC=b,AD=c,则此三棱锥的外接球的半径是

分析:这是一个类比推理的题,在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由已知在平面几何中在△ABC中,若∠C=90°,AC=b,BC=a,则△ABC的外接圆的半径r=
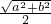
,我们可以类比这一性质,推理出在空间中有三条侧棱两两垂直的四面体A-BCD中类似的结论.
解答:由平面图形的性质类比推理空间图形的性质时
一般是由点的性质类比推理到线的性质,
由线的性质类比推理到面的性质,
由圆的性质推理到球的性质.
由已知在平面几何中,△ABC中,若∠C=90°,AC=b,BC=a,则△ABC的外接圆的半径r=
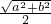
,
我们可以类比这一性质,推理出:
取空间中有三条侧棱两两垂直的四面体A-BCD,且AB=a,AC=b,AD=c,则此三棱锥的外接球的半径是

.
故答案为:取空间中有三条侧棱两两垂直的四面体A-BCD,且AB=a,AC=b,AD=c,则此三棱锥的外接球的半径是

.
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

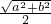 ,把上面的结论推广到空间,写出相类似的结论________.
,把上面的结论推广到空间,写出相类似的结论________.
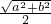 ,我们可以类比这一性质,推理出在空间中有三条侧棱两两垂直的四面体A-BCD中类似的结论.
,我们可以类比这一性质,推理出在空间中有三条侧棱两两垂直的四面体A-BCD中类似的结论.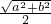 ,
, .
. .
.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案