
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,点
,点![]() 是椭圆上的一个动点,
是椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)已知点![]() ,问是否存在直线
,问是否存在直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,若存在,求出直线
,若存在,求出直线![]() 斜率的取值范围;若不存在,说明理由.
斜率的取值范围;若不存在,说明理由.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() .四边形
.四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
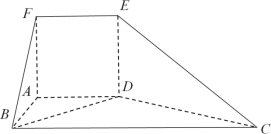
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() 若存在,求
若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“北京八分钟”在韩国平昌冬奥会惊艳亮相,冬奥会正式进入了北京周期,全社会对冬奥会的热情空前高涨.
(1)为迎接冬奥会,某社区积极推动冬奥会项目在社区青少年中的普及,并统计了近五年来本社区冬奥项目青少年爱好者的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年),列表如下:
(单位:年),列表如下:

依据表格给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).
并加以说明(计算结果精确到0.01).
(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式 ,参考数据
,参考数据![]() .
.
(2)某冰雪运动用品专营店为吸引广大冰雪爱好者,特推出两种促销方案.
方案一:每满600元可减100元;
方案二:金额超过600元可抽奖三次,每次中奖的概率同为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折. v
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折. v
两位顾客都购买了1050元的产品,并且都选择第二种优惠方案,求至少有一名顾客比选择方案一更优惠的概率;
②如果你打算购买1000元的冰雪运动用品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x),且对任意实数x都有f(x+2)=f(x),当x∈[0,1]时,f(x)=x2,若在区间[﹣3,3]内,函数g(x)=f(x)﹣kx﹣3k有6个零点,则实数k的取值范围为__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线![]() 与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 过点
过点![]() 且与直线
且与直线![]() 垂直,直线
垂直,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,动点
轴对称,动点![]() 满足
满足![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,问
,问![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 与抛物线
与抛物线![]() 的一个公共点,且椭圆与抛物线具有一个相同的焦点
的一个公共点,且椭圆与抛物线具有一个相同的焦点![]() .
.
(1)求椭圆![]() 及抛物线
及抛物线![]() 的方程;
的方程;
(2)设过![]() 且互相垂直的两动直线
且互相垂直的两动直线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值
面积的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com