
【题目】“![]() ”是“对任意的正数
”是“对任意的正数![]() ,
, ![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】分析:根据基本不等式,我们可以判断出“![]() ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+![]() ≥1”与“对任意的正数x,2x+
≥1”与“对任意的正数x,2x+![]() ≥1”?“a=
≥1”?“a=
”真假,进而根据充要条件的定义,即可得到结论.
解答:解:当“a=![]() ”时,由基本不等式可得:
”时,由基本不等式可得:
“对任意的正数x,2x+![]() ≥1”一定成立,
≥1”一定成立,
即“a=![]() ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+![]() ≥1”为真命题;
≥1”为真命题;
而“对任意的正数x,2x+![]() ≥1的”时,可得“a≥
≥1的”时,可得“a≥![]() ”
”
即“对任意的正数x,2x+![]() ≥1”?“a=
≥1”?“a=![]() ”为假命题;
”为假命题;
故“a=![]() ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+![]() ≥1的”充分不必要条件
≥1的”充分不必要条件
故选A
【题型】单选题
【结束】
9
【题目】如图是一几何体的平面展开图,其中![]() 为正方形,
为正方形, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,在此几何体中,给出下面四个结论:①直线
的中点,在此几何体中,给出下面四个结论:①直线![]() 与直线
与直线![]() 异面;②直线
异面;②直线![]() 与直线
与直线![]() 异面;③直线
异面;③直线![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() .
.
其中一定正确的选项是( )

A. ①③ B. ②③ C. ②③④ D. ①③④
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是![]() ,D是AC的中点。
,D是AC的中点。

(1)求证:B1C∥平面A1BD;
(2)求二面角A1-BD-A的大小;
(3)在线段AA1上是否存在一点E,使得平面B1C1E⊥平面A1BD,若存在,求出AE的长;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中(![]() 为坐标原点),已知两点
为坐标原点),已知两点![]() ,
,![]() ,且三角形
,且三角形![]() 的内切圆为圆
的内切圆为圆![]() ,从圆
,从圆![]() 外一点
外一点![]() 向圆引切线
向圆引切线![]() ,
,![]() 为切点。
为切点。
(1)求圆![]() 的标准方程.
的标准方程.
(2)已知点![]() ,且
,且![]() ,试判断点
,试判断点![]() 是否总在某一定直线
是否总在某一定直线![]() 上,若是,求出直线
上,若是,求出直线![]() 的方程;若不是,请说明理由.
的方程;若不是,请说明理由.
(3)已知点![]() 在圆
在圆![]() 上运动,求
上运动,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某奶茶公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的奶茶共5 杯,其颜色完全相同,并且其中3杯为![]() 奶茶,另外2杯为
奶茶,另外2杯为![]() 奶茶,公司要求此员工一一品尝后,从5杯奶茶中选出2杯奶茶.若该员工2杯都选
奶茶,公司要求此员工一一品尝后,从5杯奶茶中选出2杯奶茶.若该员工2杯都选![]() 奶茶,则评为优秀;若2 杯选对1杯
奶茶,则评为优秀;若2 杯选对1杯![]() 奶茶,则评为良好;否则评为及格.假设此人对
奶茶,则评为良好;否则评为及格.假设此人对![]() 和
和![]() 两种奶茶没有鉴别能力.
两种奶茶没有鉴别能力.
(Ⅰ)求此人被评为优秀的概率;(Ⅱ)求此人被评为良好及以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,
, ![]() 为直线
为直线![]() 上一点,线段
上一点,线段![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() __________.
__________.
【答案】![]()
【解析】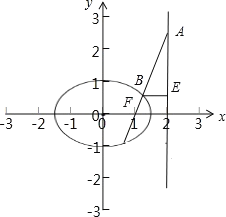
由条件椭圆![]() :
: ![]() ∴
∴![]()
椭圆的右焦点为F,可知F(1,0),
设点A的坐标为(2,m),则![]() =(1,m),
=(1,m),
∴![]() ,
,
∴点B的坐标为![]() ,
,
∵点B在椭圆C上,
∴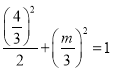 ,解得:m=1,
,解得:m=1,
∴点A的坐标为(2,1),![]() .
.
答案为: ![]() .
.
【题型】填空题
【结束】
16
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 与
与![]() 交于点
交于点![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的正切值为__________.
所成角的正切值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]()
(1)证明函数f ( x )的图象关于![]() 轴对称;
轴对称;
(2)判断![]() 在
在![]() 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明;
(3)当x∈[1,2]时函数f (x )的最大值为![]() ,求此时a的值。
,求此时a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com