
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() .以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
.以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 的方程为
的方程为![]() ,求证:直线
,求证:直线![]() 与椭圆
与椭圆![]() 有且只有一个交点.
有且只有一个交点.
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】试题分析:
(1)利用题意求得![]() ,
, ![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(2)首先讨论当![]() 的情况,否则联立直线与椭圆的方程,结合直线的特点整理可得直线
的情况,否则联立直线与椭圆的方程,结合直线的特点整理可得直线![]() 与椭圆
与椭圆![]() 有且只有一个交点.
有且只有一个交点.
试题解析:(Ⅰ)依题意,设椭圆![]() 的方程为
的方程为![]() ,焦距为
,焦距为![]() ,
,
由题设条件知, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,或
,或![]() ,
, ![]() (经检验不合题意舍去),
(经检验不合题意舍去),
故椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)当![]() 时,由
时,由![]() ,可得
,可得![]() ,
,
当![]() ,
, ![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 有且只有一个交点
有且只有一个交点![]() .
.
当![]() ,
, ![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 有且只有一个交点
有且只有一个交点![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,联立方程组
,联立方程组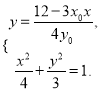
消去![]() ,得
,得![]() .①
.①
由点![]() 为曲线
为曲线![]() 上一点,得
上一点,得![]() ,可得
,可得![]() .
.
于是方程①可以化简为![]() ,解得
,解得![]() ,
,
将![]() 代入方程
代入方程![]() 可得
可得![]() ,故直线
,故直线![]() 与曲线
与曲线![]() 有且有一个交点
有且有一个交点![]() ,
,
综上,直线![]() 与曲线
与曲线![]() 有且只有一个交点,且交点为
有且只有一个交点,且交点为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知顶点在原点,焦点在x轴上的抛物线被直线y=2x+1截得的弦长为 ![]() .
.
(1)求抛物线的方程;
(2)若抛物线与直线y=2x﹣5无公共点,试在抛物线上求一点,使这点到直线y=2x﹣5的距离最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sin
sin ![]() ,1),
,1), ![]() =(cos
=(cos ![]() ,cos2
,cos2 ![]() ).
).
(Ⅰ)若 ![]()
![]() =1,求cos(
=1,求cos( ![]() ﹣x)的值;
﹣x)的值;
(Ⅱ)记f(x)= ![]()
![]() ,在△ABC中,A、B、C的对边分别为a、b、c,且满足(2a﹣c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,A、B、C的对边分别为a、b、c,且满足(2a﹣c)cosB=bcosC,求函数f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(1+x)﹣log2(1﹣x),g(x)=log2(1+x)+log2(1﹣x).
(1)判断函数f(x)奇偶性并证明;
(2)判断函数f(x)单调性并用单调性定义证明;
(3)求函数g(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点为
的左右焦点为![]() ,其离心率为
,其离心率为![]() ,又抛物线
,又抛物线![]() 在点
在点![]() 处的切线恰好过椭圆
处的切线恰好过椭圆![]() 的一个焦点.
的一个焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 斜率为
斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 的斜率分别为
的斜率分别为![]() ,是否存在常数
,是否存在常数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )
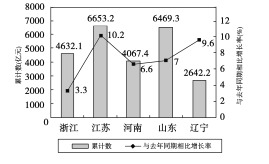
①2017年第一季度 ![]() 总量和增速均居同一位的省只有1个;
总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位是江苏、山东、浙江;
总量前三位是江苏、山东、浙江;
④2016年同期浙江的![]() 总量也是第三位.
总量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体,关于其结构特征,下列说法不正确的是( )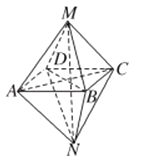
A.该几何体是由两个同底的四棱锥组成的几何体
B.该几何体有12条棱、6个顶点
C.该几何体有8个面,并且各面均为三角形
D.该几何体有9个面,其中一个面是四边形,其余均为三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
设函数f(x)=alnx﹣bx2(x>0).
(1)若函数f(x)在x=1处于直线![]() 相切,求函数f(x)在
相切,求函数f(x)在![]() 上的最大值;
上的最大值;
(2)当b=0时,若不等式f(x)≥m+x对所有的a∈[1,![]() ],x∈[1,e2]都成立,求实数m的取值范围.
],x∈[1,e2]都成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的角A、B、C所对的边分别是a、b、c,设向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ∥
∥ ![]() ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形;
(2)若 ![]() ⊥
⊥ ![]() ,边长c=2,角C=
,边长c=2,角C= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com