
【题目】(1)求过点P(2,3),且在两坐标轴上的截距相等的直线方程.
(2)已知直线l平行于直线4x+3y-7=0,直线l与两坐标轴围成的三角形的周长是15,求直线l的方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】
(1)分当直线过原点和直线不过原点两种情况求直线的方程.(2) 设直线l的方程为y=-![]() x+b,再根据直线l与两坐标轴围成的三角形的周长是15得到
x+b,再根据直线l与两坐标轴围成的三角形的周长是15得到![]() ,解方程即得b的值,即得直线l的方程.
,解方程即得b的值,即得直线l的方程.
(1)当直线过原点时,过点(2,3)的直线为y=![]() x;
x;
当直线不过原点时,设直线方程为![]() (a≠0),直线过点(2,3),
(a≠0),直线过点(2,3),
解得a=5,所以直线方程为![]() .
.
故过点P(2,3),且在两坐标轴上的截距相等的直线方程为3x-2y=0和x+y-5=0.
(2)∵直线l与直线4x+3y-7=0平行,
∴kl=![]() .
.
设直线l的方程为y=-![]() x+b,
x+b,
则直线l与x轴的交点为A![]() ,与y轴的交点为B(0,b),
,与y轴的交点为B(0,b),
∴![]() .
.
∵直线l与两坐标轴围成的三角形周长是15,
∴![]() .
.
∴|b|=5,∴b=±5.
∴直线l的方程是y=-![]() x±5,即4x+3y ±15=0.
x±5,即4x+3y ±15=0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点, ![]() 轴正半轴为极轴建立极坐标系,已知圆
轴正半轴为极轴建立极坐标系,已知圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若
为参数),若![]() 与
与![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)1.
;(2)1.
【解析】试题分析:(1)先根据![]() 将圆
将圆![]() 的极坐标方程化为直角坐标方程;(2)先将直线参数方程调整化简
的极坐标方程化为直角坐标方程;(2)先将直线参数方程调整化简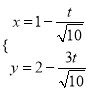 ,再将直线参数方程代入圆直角坐标方程,根据参数几何意义得
,再将直线参数方程代入圆直角坐标方程,根据参数几何意义得![]() ,最后利用韦达定理求解
,最后利用韦达定理求解
试题解析:(Ⅰ)由![]() ,得
,得![]() ,
,
![]()
(Ⅱ)把![]() ,
, ![]()
代入上式得![]() ,
,
∴![]() ,则
,则![]() ,
, ![]() ,
,
![]()
![]()
![]() .
.
【题型】解答题
【结束】
23
【题目】证明:(Ⅰ)已知![]() 是正实数,且
是正实数,且![]() .求证:
.求证: ![]() ;
;
(Ⅱ)已知![]() ,且
,且![]() ,
, ![]() ,
, ![]() .求证:
.求证: ![]() 中至少有一个是负数.
中至少有一个是负数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() :
:![]() 上任意一点,点
上任意一点,点![]() 与点
与点![]() 关于原点对称,线段
关于原点对称,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于
交于![]() 点.
点.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() 使以
使以![]() 为直径的圆恒过这个点?若存在,求出点
为直径的圆恒过这个点?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.

(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆E的极坐标方程为ρ=4sinθ,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,取相同单位长度(其中(ρ,θ),ρ≥0,θ∈[0,2π))).
(1)直线l过原点,且它的倾斜角α= ![]() ,求l与圆E的交点A的极坐标(点A不是坐标原点);
,求l与圆E的交点A的极坐标(点A不是坐标原点);
(2)直线m过线段OA中点M,且直线m交圆E于B、C两点,求||MB|﹣|MC||的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种大型商品,A,B两地都有出售,且价格相同,某地居民从两地之一购得商品后,运回的费用是:每单位距离A地的运费是B地运费的3倍.已知A,B两地相距10 km,顾客选A或B地购买这件商品的标准是:包括运费和价格的总费用较低.求A,B两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
高峰时间段用电价格表 | 低谷时间段用电价格表 | ||
高峰月用 电量(单 位:千瓦时) | 高峰电价 (单位:元/ 千瓦时) | 低谷月用 电量(单位: 千瓦时) | 低谷电价 (单位:元/ 千瓦时) |
50及以下 的部分 | 0.568 | 50及以下 的部分 | 0.288 |
超过 50 至 200 的部分 | 0.598 | 超过 50 至 200 的部分 | 0.318 |
超过200 的部分 | 0.668 | 超过 200 的部分 | 0.388 |
若某家庭5月份的高峰时间段用电量为 200 千瓦时,低谷时间段用电量为 100 千瓦时,则按这种计费方式该家庭本月应付的电费为____________元.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为G(
(百台),其总成本为G(![]() )(万元),其中固定成本为
)(万元),其中固定成本为![]() 万元,并且每生产
万元,并且每生产![]() 百台的生产成本为
百台的生产成本为![]() 万元(总成本 = 固定成本 + 生产成本);销售收入R(
万元(总成本 = 固定成本 + 生产成本);销售收入R(![]() )(万元)满足:
)(万元)满足:![]() ,假定该产品产销平衡,那么根据上述统计规律:
,假定该产品产销平衡,那么根据上述统计规律:
(Ⅰ)要使工厂有赢利,产量![]() 应控制在什么范围?
应控制在什么范围?
(Ⅱ)工厂生产多少台产品时,可使赢利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com