
【题目】在△ABC中,已知内角A,B,C所对的边分别为a,b,c,向量m=(2sin B,- ![]() ),n=
),n=![]() ,且m∥n.
,且m∥n.
(1)求锐角B的大小;
(2)如果b=2,求△ABC的面积S△ABC的最大值.
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】设矩形ABCD(AB>AD)的周长为24,把△ABC沿AC向△ADC折叠,AB折过去后交DC于点P,设AB=x,求△ADP的最大面积及相应x的值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位![]() 名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组
名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
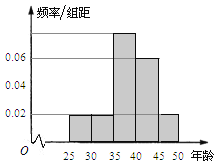
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(I)现要从年龄低于40岁的员工中用分层抽样的方法抽取12人,则年龄在第![]() 组的员工人数分别是多少?
组的员工人数分别是多少?
(II)为了交流读书心得,现从上述![]() 人中再随机抽取
人中再随机抽取![]() 人发言,设
人发言,设![]() 人中年龄在
人中年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(III)为了估计该单位员工的阅读倾向,现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查,调查结果如下表所示:(单位:人)
喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
男 | 14 | 4 | 18 |
女 | 8 | 14 | 22 |
合计 | 22 | 18 | 40 |
根据表中数据,我们能否有![]() 的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
附:![]() ,其中
,其中![]()
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料![]() ,五合板
,五合板![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料![]() ,五合板
,五合板![]() ,生产每个书橱需要方木料
,生产每个书橱需要方木料![]() ,五合板
,五合板![]() ,出售一张书桌可获利润
,出售一张书桌可获利润![]() 元,出售一个书橱可获利润
元,出售一个书橱可获利润![]() 元.
元.
(1)如果只安排生产书桌,可获利润多少?
(2)如果只安排生产书橱,可获利润多少?
(3)怎样安排生产可使所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用分期付款的方式购买某家用电器一件,价格为1 150元,购买当天先付150元,以后每月这一天还款一次,每次还款数额相同,20个月还清,月利率为1%,按复利计算.若交付150元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?每月还款多少元?(最后结果保留4个有效数字)
参考数据:(1+1%)19=1.208,(1+1%)20=1.220,(1+1%)21=1.232.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋中装有大小相同的2个白球、2个红球和1个黄球.一项游戏规定:每个白球、红球和黄球的分值分别是0分、1分和2分,每一局从袋中一次性取出三个球,将3个球对应的分值相加后称为该局的得分,计算完得分后将球放回袋中.当出现第![]() 局得
局得![]() 分(
分(![]() )的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
)的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
(1)求在一局游戏中得3分的概率;
(2)求游戏结束时局数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1.设命题p:函数y=loga(x+1)在(0,+∞)内单调递减;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.若p或q为真,p且q为假,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com