
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池![]() 及其矩形附属设施
及其矩形附属设施![]() ,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为
,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形的一边
,矩形的一边![]() 在直径上,点
在直径上,点![]() 、
、![]() 、
、![]() 、
、![]() 在圆周上,
在圆周上,![]() 、
、![]() 在边
在边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)怎样设计才能符合园林局的要求?

科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中, ![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() .
.
(1)求证:数列![]() 为等差数列,并求
为等差数列,并求![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() 为非零整数
为非零整数![]() ,是否存在
,是否存在![]() 的值,使得对任意
的值,使得对任意![]() 恒成立,若存在求出
恒成立,若存在求出![]() 的值,若不存在说明理由.
的值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
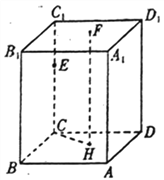
【题目】如图所示,直平行六面体![]() 中,
中,![]() 为棱
为棱![]() 上任意一点,
上任意一点,![]() 为底面
为底面![]() (除
(除![]() 外)上一点,已知
外)上一点,已知![]() 在底面
在底面![]() 上的射影为
上的射影为![]() ,若再增加一个条件,就能得到
,若再增加一个条件,就能得到![]() ,现给出以下条件:
,现给出以下条件:
①![]() ;②
;②![]() 在
在![]() 上;③
上;③![]() 平面
平面![]() ;④直线
;④直线![]() 和
和![]() 在平面
在平面![]() 的射影为同一条直线.其中一定能成为增加条件的是__________.(把你认为正确的都填上)
的射影为同一条直线.其中一定能成为增加条件的是__________.(把你认为正确的都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有命题: ①y=|sinx﹣ ![]() |的周期是π;
|的周期是π;
②y=sinx+sin|x|的值域是[0,2];
③方程cosx=lgx有三解;
④ω为正实数,y=2sinωx在 ![]() 上递增,那么ω的取值范围是
上递增,那么ω的取值范围是 ![]() ;
;
⑤在y=3sin(2x+ ![]() )中,若f(x1)=f(x2)=0,则x1﹣x2必为π的整数倍;
)中,若f(x1)=f(x2)=0,则x1﹣x2必为π的整数倍;
⑥若A、B是锐角△ABC的两个内角,则点P(cosB﹣sinA,sinB﹣cosA在第二象限;
⑦在△ABC中,若 ![]() ,则△ABC钝角三角形.其中真命题个数为( )
,则△ABC钝角三角形.其中真命题个数为( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元).设购买某商品得到的实际折扣率![]() .设某商品标价为
.设某商品标价为![]() 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为![]() .
.
(Ⅰ)写出当![]() 时,
时, ![]() 关于
关于![]() 的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(Ⅱ)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() (万元),若年产量不足
(万元),若年产量不足![]() 千件,
千件, ![]() 的图像是如图的抛物线,此时
的图像是如图的抛物线,此时![]() 的解集为
的解集为![]() ,且
,且![]() 的最小值是
的最小值是![]() ,若年产量不小于
,若年产量不小于![]() 千件,
千件, ![]() ,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,侧面
为矩形,侧面![]() 为正三角形,且平面
为正三角形,且平面![]()
![]() 平面,
平面, ![]() 为
为![]() 中点,
中点, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的平面角大小
的平面角大小![]() 满足
满足![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com