
如图,在矩形 中,点
中,点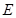 为边
为边 上的点,点
上的点,点 为边
为边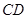 的中点,
的中点,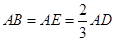 ,现将
,现将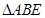 沿
沿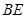 边折至
边折至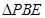 位置,且平面
位置,且平面 平面
平面 .
.
(1) 求证:平面 平面
平面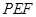 ;
;
(2) 求二面角 的大小.
的大小.
(1)详见解析;(2) .
.
解析试题分析:(1) 利用直角三角形,先证明折前有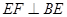 ,折后这个垂直关系没有改变,然后由平面
,折后这个垂直关系没有改变,然后由平面 平面
平面 的性质证明
的性质证明 平面
平面 ,最后由面面垂直的判定定理即可证明平面
,最后由面面垂直的判定定理即可证明平面 平面
平面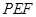 ;(2)为方便计算,不妨设
;(2)为方便计算,不妨设 ,先以
,先以 为原点,以
为原点,以 方向为
方向为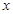 轴,以
轴,以 方向为
方向为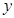 轴,以与平面
轴,以与平面 向上的法向量同方向为
向上的法向量同方向为 轴,建立空间直角坐标系,写给相应点的坐标,然后分别求出平面
轴,建立空间直角坐标系,写给相应点的坐标,然后分别求出平面 和平面
和平面 的一个法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.
的一个法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.
试题解析:(1) 证明:由题可知:折前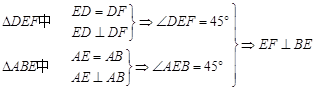 ,这个垂直关系,折后没有改变
,这个垂直关系,折后没有改变
故折后有
(2)不妨设 ,以
,以 为原点,以
为原点,以 方向为
方向为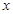 轴,以
轴,以 方向为
方向为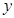 轴,以与平面
轴,以与平面 向上的法向量同方向为
向上的法向量同方向为 轴,建立空间直角坐标系 7分
轴,建立空间直角坐标系 7分
则
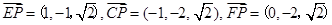
设平面 和平面
和平面 的法向量分别为
的法向量分别为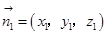 ,
,
由 及
及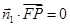 可得到
可得到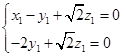 即
即 ,不妨取
,不妨取

又由 及
及 可得到
可得到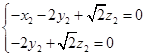 即
即
不妨取 9分
9分 11分
11分
综上所述,二面角 大小为
大小为 12分.
12分.
考点:1.线线垂直的证明;2. 线面垂直、面面垂直的判定与性质;3.空间向量在解决空间角中的运用问题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,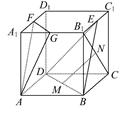
求证:(1)MN∥平面CDD1C1.
(2)平面EBD∥平面FGA.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.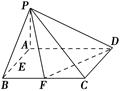
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在正三棱柱ABC—A1B1C1中, .
.
(1)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(2)在线段 上是否存在点
上是否存在点 ?使得二面角
?使得二面角 的大小为60°,若存在,求出
的大小为60°,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面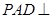 底面
底面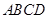 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形, ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.
(1)求证:EF//平面PAD;
(2)求证:平面 平面
平面 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,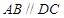 ,
, ,DC=1,AB=2,PA⊥平面ABCD,PA=1.
,DC=1,AB=2,PA⊥平面ABCD,PA=1.
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com