
【题目】已知函数![]() .
.
(1)令![]() ,若
,若![]() 在区间
在区间![]() 上不单调,求
上不单调,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,
,![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() ,
,![]() 满足条件
满足条件![]() ,
,![]() .试比较
.试比较![]() 与0的关系,并给出理由
与0的关系,并给出理由
【答案】(1)![]() (2)见解析.
(2)见解析.
【解析】
(1)先求得![]() ,因为g(x)在区间(0,3)上不单调,所以g'(x)=0在(0,3)上有实数解,且无重根.由g'(x)=0,求得
,因为g(x)在区间(0,3)上不单调,所以g'(x)=0在(0,3)上有实数解,且无重根.由g'(x)=0,求得![]() ,由此可得a的范围.(2)由题意可得,f(x)﹣mx=0有两个实根x1,x2,化简可得
,由此可得a的范围.(2)由题意可得,f(x)﹣mx=0有两个实根x1,x2,化简可得![]() .可得h′(α
.可得h′(α![]() +β
+β![]() )
)![]() ,由条件知(2α﹣1)(
,由条件知(2α﹣1)(![]() )≤0,利用分析法结合构造函数证明h′(α
)≤0,利用分析法结合构造函数证明h′(α![]() +β
+β![]() )
)![]()
(1)因为![]() ,所以
,所以![]() ,
,
因为![]() 在区间
在区间![]() 上不单调,所以
上不单调,所以![]() 在
在![]() 上有实数解,且无重根,
上有实数解,且无重根,
由![]() ,有
,有![]() ,
,![]() ,令t=x+1>4
,令t=x+1>4
则y=2(t+![]() 在t>4单调递增,故
在t>4单调递增,故![]()
(2)∵![]() ,又
,又![]() 有两个实根
有两个实根![]() ,
,![]() ,
,
∴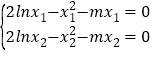 ,两式相减,得
,两式相减,得![]() ,
,
∴![]() ,
,
于是![]()
![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
要证:![]() ,只需证:
,只需证:![]()
只需证:![]() .(*)
.(*)
令![]() ,∴(*)化为
,∴(*)化为![]() ,只需证
,只需证![]()
![]() ∵
∵![]() 在
在![]() 上单调递增,
上单调递增,![]() ,∴
,∴![]() ,即
,即![]() .
.
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】空气质量指数![]() 是检测空气质量的重要参数,其数值越大说明空气污染状况越严重,空气质量越差.某地环保部门统计了该地区某月1日至24日连续24天的空气质量指数
是检测空气质量的重要参数,其数值越大说明空气污染状况越严重,空气质量越差.某地环保部门统计了该地区某月1日至24日连续24天的空气质量指数![]() ,根据得到的数据绘制出如图所示的折线图,则下列说法错误的是( )
,根据得到的数据绘制出如图所示的折线图,则下列说法错误的是( )
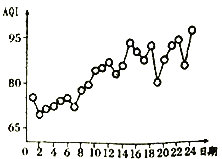
A. 该地区在该月2日空气质量最好
B. 该地区在该月24日空气质量最差
C. 该地区从该月7日到12日![]() 持续增大
持续增大
D. 该地区的空气质量指数![]() 与这段日期成负相关
与这段日期成负相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系.已知曲线
轴非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数)
为参数)
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,若
,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣1=0与直线x﹣2y+1=0交于点P.
(Ⅰ)求过点P且平行于直线3x+4y﹣15=0的直线![]() 的方程;(结果写成直线方程的一般式)
的方程;(结果写成直线方程的一般式)
(Ⅱ)求过点P并且在两坐标轴上截距相等的直线![]() 方程(结果写成直线方程的一般式)
方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①在函数![]() 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为![]() ;
;
②函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
③“![]() 且
且![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
④在![]() 中,若
中,若![]() ,则角
,则角![]() 等于
等于![]() 或
或![]() .
.
其中是真命题的序号为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中,过点
中,过点![]() 的直线l的参数方程为
的直线l的参数方程为![]() (t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() 与曲线C相交于不同的两点M,N.
与曲线C相交于不同的两点M,N.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
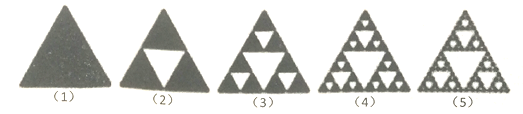
【题目】谢尔宾斯基三角形(Sierpinski triangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出.在一个正三角形中,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色三角形代表挖去的部分,黑色三角形为剩下的部分,我们称此三角形为谢尔宾斯基三角形.若在图(3)内随机取一点,则此点取自谢尔宾斯基三角形的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com