
【题目】已知椭圆 ![]() +
+ ![]() =1(a>b>0)右顶点与右焦点的距离为
=1(a>b>0)右顶点与右焦点的距离为 ![]() ﹣1,短轴长为2
﹣1,短轴长为2 ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)过左焦点F的直线与椭圆分别交于A、B两点,若三角形OAB的面积为 ![]() ,求直线AB的方程.
,求直线AB的方程.
【答案】解:(Ⅰ)由题意, 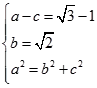 ,解得a=
,解得a= ![]() ,c=1. 即椭圆方程为
,c=1. 即椭圆方程为 ![]() =1
=1
(Ⅱ)当直线AB与x轴垂直时,|AB|= ![]() ,此时S=
,此时S= ![]() 不符合题意,故舍掉;
不符合题意,故舍掉;
当直线AB与x轴不垂直时,设直线 AB的方程为:y=k(x+1),代入消去y得:(2+3k2)x2+6k2x+(3k2﹣6)=0.
设A(x1 , y1),B(x2 , y2),则 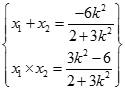 ,所以|AB|=
,所以|AB|= ![]() .
.
原点到直线的AB距离d= ![]() ,
,
所以三角形的面积S= 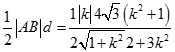 .
.
由S= ![]() 可得k2=2,∴k=±
可得k2=2,∴k=± ![]() ,
,
所以直线AB: ![]() =0或AB:
=0或AB: ![]() =0
=0
【解析】(Ⅰ)根据椭圆右顶点与右焦点的距离为 ![]() ,短轴长为
,短轴长为 ![]() ,可得
,可得 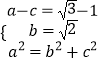 ,由此,即可求得椭圆方程;(Ⅱ)当直线AB与x轴垂直时,
,由此,即可求得椭圆方程;(Ⅱ)当直线AB与x轴垂直时, ![]() ,此时
,此时 ![]() 不符合题意;当直线AB与x轴不垂直时,设直线 AB的方程为:y=k(x+1),代入消去y得,进而可求三角形的面积,利用
不符合题意;当直线AB与x轴不垂直时,设直线 AB的方程为:y=k(x+1),代入消去y得,进而可求三角形的面积,利用 ![]() ,即可求出直线AB的方程.
,即可求出直线AB的方程.
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).


科目:高中数学 来源: 题型:
【题目】已知定圆C:x2+(y﹣3)2=4,定直线m;x+3y+6=0,过A(﹣1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,
(1)当l与m垂直时,求出N点的坐标,并证明:l过圆心C;
(2)当|PQ|=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体A﹣BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2 ![]() .M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC. 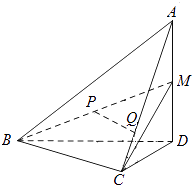
(1)证明:PQ∥平面BCD;
(2)若二面角C﹣BM﹣D的大小为60°,求∠BDC的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=|x﹣1|,若方程f(x)= ![]() 有4个不相等的实根,则实数a的取值范围是( )
有4个不相等的实根,则实数a的取值范围是( )
A.(﹣ ![]() ,1)
,1)
B.( ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.(﹣1, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可参加抽奖,抽奖有两种方案可供选择. 方案一:从装有4个红球和2个白球的不透明箱中,随机摸出2个球,若摸出的2个球都是红球则中奖,否则不中奖;
方案二:掷2颗骰子,如果出现的点数至少有一个为4则中奖,否则不中奖.(注:骰子(或球)的大小、形状、质地均相同)
(Ⅰ)有顾客认为,在方案一种,箱子中的红球个数比白球个数多,所以中奖的概率大于 ![]() .你认为正确吗?请说明理由;
.你认为正确吗?请说明理由;
(Ⅱ)如果是你参加抽奖,你会选择哪种方案?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程(m2﹣2m﹣3)x+(2m2+m﹣1)y+6﹣2m=0(m∈R).
(1)求该方程表示一条直线的条件;
(2)当m为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
(3)已知方程表示的直线l在x轴上的截距为﹣3,求实数m的值;
(4)若方程表示的直线l的倾斜角是45°,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E的中心为原点,P(3,0)是E的焦点,过P的直线l与E相交于A,B两点,且AB的中点为N(﹣12,﹣15),则E的方程式为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据环保部通报,2016年10月24日起,京津冀周边雾霾又起,为此,环保部及时提出防控建议,推动应对工作由过去“大水漫灌式”的减排方式转变为实现精确打击.某燃煤企业为提高应急联动的同步性,新购置并安装了先进的废气处理设备,使产生的废气经过过滤后排放,以降低对大气环境的污染,已知过滤后废气的污染物数量N(单位:mg/L)与过滤时间t(单位:小时)间的关系为N(t)=N0e﹣λt(N0 , λ均为非零常数,e为自然对数的底数)其中N0为t=0时的污染物数量,若经过5小时过滤后污染物数量为 ![]() N0 .
N0 .
(1)求常数λ的值;
(2)试计算污染物减少到最初的10%至少需要多少时间?(精确到1小时) 参考数据:ln3≈1.10,ln5≈1.61,ln10≈2.30.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2﹣ ![]() 在其定义域内的一个子区间(k﹣1,k+1)内不是单调函数,则实数k的取值范围( )
在其定义域内的一个子区间(k﹣1,k+1)内不是单调函数,则实数k的取值范围( )
A.[1,+∞)
B.[1, ![]() )
)
C.[1,+2)
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com