
【题目】两个人射击,甲射击一次中靶概率是![]() ,乙射击一次中靶概率是
,乙射击一次中靶概率是![]() .
.
(1)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(2)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面 ABCD为矩形,侧面为正三角形,且平面
中,底面 ABCD为矩形,侧面为正三角形,且平面![]() 平面
平面 ![]() E 为 PD 中点,AD=2.
E 为 PD 中点,AD=2.
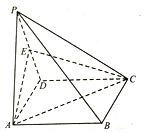
(1)证明平面AEC丄平面PCD;
(2)若二面角![]() 的平面角
的平面角![]() 满足
满足![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月18日,举世瞩目的第18届亚运会在印尼首都雅加达举行,为了丰富亚运会志愿者的业余生活,同时鼓励更多的有志青年加入志愿者行列,大会主办方决定对150名志愿者组织一次有关体育运动的知识竞赛(满分120分)并计划对成绩前15名的志愿者进行奖励,现将所有志愿者的竞赛成绩制成频率分布直方图,如图所示,若第三组与第五组的频数之和是第二组的频数的3倍,试回答以下问题:
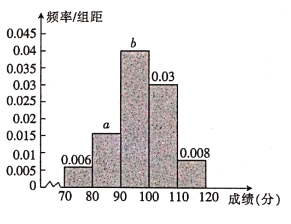
(1)求图中![]() 的值;
的值;
(2)求志愿者知识竞赛的平均成绩;
(3)从受奖励的15人中按成绩利用分层抽样抽取5人,再从抽取的5人中,随机抽取2人在主会场服务,求抽取的这2人中其中一人成绩在![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(江苏省南京师大附中2018届高三高考考前模拟考试数学试题)已知等差数列{an}和等比数列{bn}均不是常数列,若a1=b1=1,且a1,2a2,4a4成等比数列, 4b2,2b3,b4成等差数列.
(1)求{an}和{bn}的通项公式;
(2)设m,n是正整数,若存在正整数i,j,k(i<j<k),使得ambj,amanbi,anbk成等差数列,求m+n的最小值;
(3)令cn=![]() ,记{cn}的前n项和为Tn,{
,记{cn}的前n项和为Tn,{![]() }的前n项和为An.若数列{pn}满足p1=c1,且对n≥2, n∈N*,都有pn=
}的前n项和为An.若数列{pn}满足p1=c1,且对n≥2, n∈N*,都有pn=![]() +Ancn,设{pn}的前n项和为Sn,求证:Sn<4+4lnn.
+Ancn,设{pn}的前n项和为Sn,求证:Sn<4+4lnn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 上一点,
上一点,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,点
,点![]() 满足
满足![]() (
(![]() 为坐标原点),点
为坐标原点),点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,是否存在定点
,是否存在定点![]() ,使得直线
,使得直线![]() 、
、![]() 的斜率之和恒为0.若存在,则求出点
的斜率之和恒为0.若存在,则求出点![]() 的坐标;若不存在,则请说明理由.
的坐标;若不存在,则请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为![]() ,且过点
,且过点![]() .点M(3,m)在双曲线上.
.点M(3,m)在双曲线上.
(1)求双曲线的方程;
(2)求证:![]() ;
;
(3)求△F1MF2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
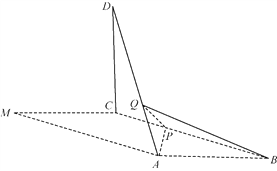
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为折痕将△
为折痕将△![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 上一点,
上一点,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度. 药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
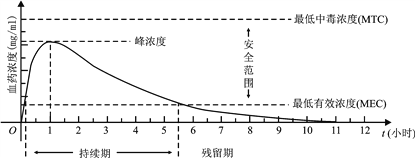
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是
A. 首次服用该药物1单位约10分钟后,药物发挥治疗作用
B. 每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
C. 每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
D. 首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com