
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 和
和![]() 中点.
中点.
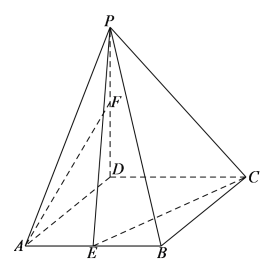
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明出四边形
,证明出四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,然后利用线面平行的判定定理可证得直线
,然后利用线面平行的判定定理可证得直线![]() 平面
平面![]() ;
;
(2)连接![]() ,推导出
,推导出![]() ,然后以点
,然后以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,利用空间向量法可求得直线
轴建立空间直角坐标系,利用空间向量法可求得直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)取![]() 的中点为
的中点为![]() ,连接
,连接![]() 、
、![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 且
且![]()
![]() 四边形
四边形![]() 是菱形,
是菱形,![]() 是
是![]() 的中点,
的中点,![]() 且
且![]() ,
,
![]() 且
且![]() ,
,![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
又![]() 面
面![]() ,
,![]() 面
面![]() ,
,![]() 直线
直线![]() 平面
平面![]() ;
;

(2)连接![]() 、
、![]() ,
,
四边形![]() 是菱形,
是菱形,![]() ,
,![]() 是等边三角形,
是等边三角形,
![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() ,
,
又![]() 面
面![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,

则![]() 、
、![]() 、
、 、
、 ,
,
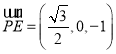 ,
, ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由 ,即
,即 ,令
,令![]() ,得
,得![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则 ,
,
因此,![]() 平面
平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(2)直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,记弦
两点,记弦![]() 的中点为
的中点为![]() ,点
,点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响.对近
(单位:千元)的影响.对近![]() 年的年宣传费
年的年宣传费![]() 和年销售量数据
和年销售量数据![]() 作了初步处理,得到下面的散点图及一些统计量的值.
作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .附:对于一组数据
.附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为 ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 在哪一个适宜作为年销售量
在哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据1小问的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() .根据2小问的结果回答下列问题:
.根据2小问的结果回答下列问题:
①2年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
②3年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三家企业产品的成本分别为10000,12000,15000,其成本构成如下图所示,则关于这三家企业下列说法错误的是( )
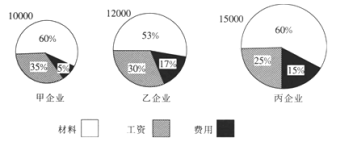
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业
C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等边![]() 的边长为3,点
的边长为3,点![]() 分别为
分别为![]() 上的点,且满足
上的点,且满足![]() (如图1),将
(如图1),将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 成直二面角,连接
成直二面角,连接![]() ,
, ![]() (如图2)
(如图2)
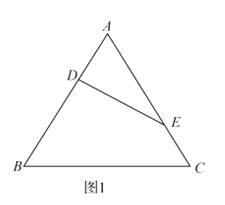
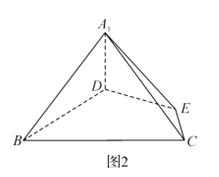
(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节期间,随着新型冠状病毒肺炎疫情在全国扩散,各省均启动重大突发公共卫生事件一级响应,采取了一系列有效的防控措施.如测量体温、有效隔离等.
(1)现从深圳市某社区的体温登记表中随机采集100个样本.据分析,人群体温近似服从正态分布![]() .若
.若![]() 表示所采集100个样本的数值在
表示所采集100个样本的数值在![]() 之外的的个数,求
之外的的个数,求![]() 及X的数学期望.
及X的数学期望.
(2)疫情期间,武汉大学中南医院重症监护室(ICU)主任彭志勇团队对138例确诊患者进行跟踪记录.为了分析并发症(complications)与重症患者(ICU)有关的可信程度,现从该团队发表在国际顶级医学期刊JAMA《美国医学会杂志》研究论文中获得相关数据.请将下列2×2列联表补充完整,并判断能否在犯错误的概率不超过0.1%的前提下认为“重症患者与并发症有关”?

附:若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式与临界值表: ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某支教队有8名老师,现欲从中随机选出2名老师参加志愿活动,
(1)若规定选出的至少有一名女老师,则共有18种不同的需安排方案,试求该支教队男、女老师的人数;
(2)在(1)的条件下,记![]() 为选出的2位老师中女老师的人数,写出
为选出的2位老师中女老师的人数,写出![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com