已知函数

满足:①定义在
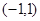
上;②当
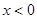
时,
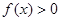
;③对于任意的
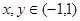
,有
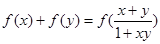
.
(1)取一个对数函数
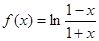
,验证它是否满足条件②,③;
(2)对于满足条件①,②,③的一般函数

,判断

是否具有奇偶性和单调性,并加以证明.
(1)当
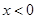
时,
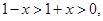
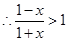
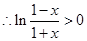
.
又
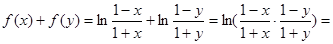
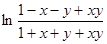
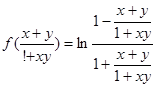
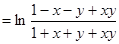
,即
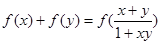
.
故
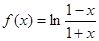
满足条件②,③.
(2)

在
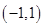
上是奇函数.

在
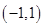
上是减函数.
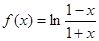
,当
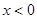
,时先计算出
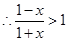
,在利用对数函数的性质,得
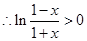
;利用对数的运算法则,得出
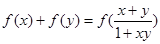
。
解:(1)当
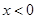
时,
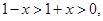
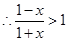
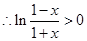
.
又
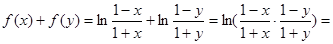
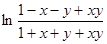
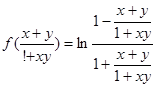
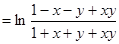
,即
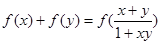
.
故
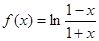
满足条件②,③.
(2)这样的函数是奇函数.
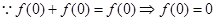
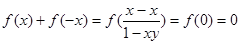
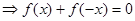
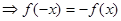
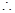

在
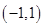
上是奇函数.
这样的函数是减函数.
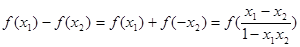
当
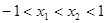
时,
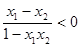
,由条件知
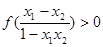
,即
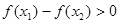
.
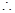

在
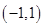
上是减函数.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知a>0,b
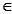
R,函数
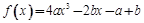
.
(Ⅰ)证明:当0≤x≤1时,
(ⅰ)函数
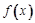
的最大值为|2a-b|﹢a;
(ⅱ)
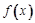
+|2a-b|﹢a≥0;
(Ⅱ) 若﹣1≤
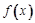
≤1对x
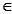
[0,1]恒成立,求a+b的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
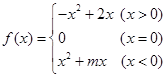
为奇函数,若函数
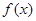
在区间
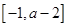
上单调递增,则
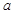
的取值范围是
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
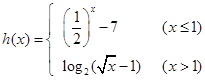
(1)判断函数
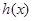
在区间
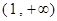
上的单调性并用定义证明;
(2)若
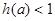
,求
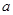
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数
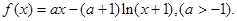
(I)设
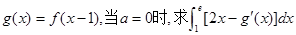
;
(II)求
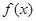
的单调区间;
(III)当
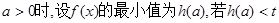
恒成立,求实数t的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
奇函数
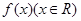
满足:
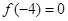
,且在区间
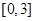
与
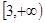
上分别递减和递增,则不等式
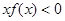
的解集为_____.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设函数
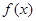
的图像关于
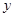
轴对称,又已知
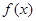
在
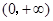
上为减函数,且
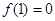
,则不等式
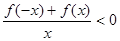
的解集为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若
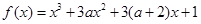
有极大值和极小值,则
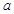
的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
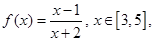
求函数
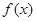
的最大值和最小值.
查看答案和解析>>

 满足:①定义在
满足:①定义在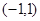 上;②当
上;②当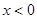 时,
时,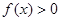 ;③对于任意的
;③对于任意的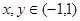 ,有
,有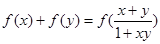 .
.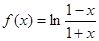 ,验证它是否满足条件②,③;
,验证它是否满足条件②,③;  ,判断
,判断 是否具有奇偶性和单调性,并加以证明.
是否具有奇偶性和单调性,并加以证明.  阅读快车系列答案
阅读快车系列答案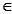 R,函数
R,函数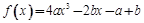 .
.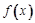 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a;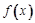 +|2a-b|﹢a≥0;
+|2a-b|﹢a≥0;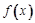 ≤1对x
≤1对x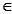 [0,1]恒成立,求a+b的取值范围.
[0,1]恒成立,求a+b的取值范围.