
分析 (1)分别求出27名男生的总分和21名女生的总分,这两个总分相加后除全班人数48,就得到这次测验全班平均分.
(2)根据已知条件,利用中位数的性质能估计全班成绩在80分以下(含80分)的同学至少有多少人.
(3)利用平均分和总位数的概念进行分析.
解答 解:(1)由已知得这次测验全班平均分$\overline{x}$=$\frac{82×27+80×21}{27+21}$=81.125≈81.13.
(2)27名男同学的中位数是75,即至少有14人得分小于或等于75,
21女同学的中位数是80,即至少有11人得分小于或等于80,
∴全班至少有25人,得分在80分以下(包括80分),
由此估计全班成绩在80分以下(含80分)的同学至少有25人.
(3)男同学的平均分与中位数差距较大,说明男同学中两极分化现象严重,
有一批同学得分较高,同时也有一半左右的同学(至少14人)得分在75分(包括75分)以下.
点评 本题考查平均数的计算,考查中位数的应用,是基础题,解题时要熟练掌握基本概念.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
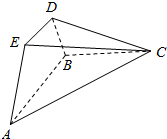 已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2.
已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.
如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
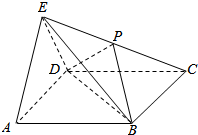 如图,在四棱锥E-ABCD中,底面ABCD为正方形,侧面EAD是正三角形,平面EAD⊥平面ABCD为正方形,P为EC的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,侧面EAD是正三角形,平面EAD⊥平面ABCD为正方形,P为EC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com